Can you answer these queries?（HDU4027+势能线段树）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4027

题目：

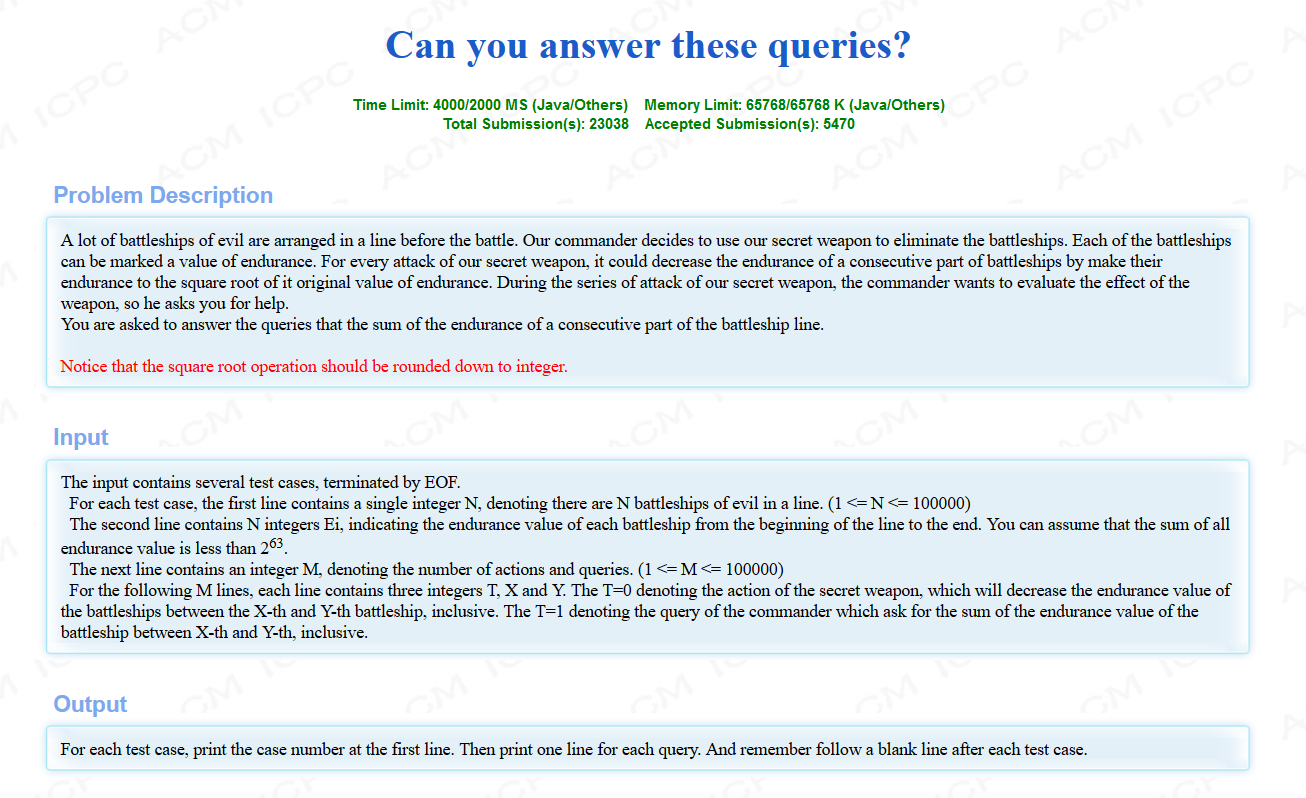
题意：n个数，每次区间更新将其数值变成它的根号倍（向下取整），区间查询数值和。

思路：易知这题的lazy标记是不好打的，但是我们发现当这个数取根号直到变成1时就不需要更新了，像这种无法打标记并且经过多次操作后就不需要操作的线段树叫做势能线段树。在需要更新时我们一直暴力到它的叶子节点，当某个区间无法更新时我们将其的flag设为0，对于某个节点的flag就等于它的左右子节点的flag取或。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef unsigned long long ull;

 #define lson i<<1,l,mid
 #define rson i<<1|1,mid+1,r
 #define bug printf("*********\n");
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = 1e8;
 const int maxn = 1e5 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f3f;

 inline int read() {//读入挂
     int ret = , c, f = ;
     for(c = getchar(); !(isdigit(c) || c == '-'); c = getchar());
     if(c == '-') f = -, c = getchar();
     for(; isdigit(c); c = getchar()) ret = ret *  + c - '';
     if(f < ) ret = -ret;
     return ret;
 }

 int n, q, op, x, y;

 struct node {
     int l, r, flag;
     ll sum;
 }segtree[maxn*];

 void push_up(int i) {
     segtree[i].sum = segtree[i*].sum + segtree[i*+].sum;
     segtree[i].flag = segtree[i*].flag | segtree[i*+].flag;
 }

 void build(int i, int l, int r) {
     segtree[i].l = l, segtree[i].r = r, segtree[i].flag = ;
     if(l == r) {
         scanf("%lld", &segtree[i].sum);
         if(segtree[i].sum <= ) segtree[i].flag = ;
         return;
     }
     int mid = (l + r) >> ;
     build(lson);
     build(rson);
     push_up(i);
 }

 void update(int i, int l, int r) {
     if(!segtree[i].flag) return;
     if(segtree[i].l == segtree[i].r) {
         if(segtree[i].flag) {
             segtree[i].sum = sqrt(segtree[i].sum);
             if(segtree[i].sum <= ) segtree[i].flag = ;
         }
         return;
     }
     int mid = (segtree[i].l + segtree[i].r) >> ;
     if(r <= mid) {
         if(segtree[i*].flag)
             update(i*, l, r);
     }
     else if(l > mid) {
         if(segtree[i*+].flag)
             update(i*+, l, r);
     }
     else {
         if(segtree[i*].flag) update(lson);
         if(segtree[i*+].flag) update(rson);
     }
     push_up(i);
 }

 ll query(int i, int l, int r) {
     if(segtree[i].l == l && segtree[i].r == r) {
         return segtree[i].sum;
     }
     int mid = (segtree[i].l + segtree[i].r) >> ;
     if(l > mid) return query(i *  + , l, r);
     else if(r <= mid) return query(i * , l, r);
     else return query(lson) + query(rson);
 }

 int main() {
     //FIN;
     int icase = ;
     while(~scanf("%d", &n)) {
         build(, , n);
         printf("Case #%d:\n", ++icase);
         scanf("%d", &q);
         while(q--) {
             scanf("%d%d%d", &op, &x, &y);
             int a = max(x, y), b = min(x, y);
             if(op == ) {
                 update(, b, a);
             } else {
                 printf("%lld\n", query(, b, a));
             }
         }
         printf("\n");
     }
     return ;
 }