HDU 5794：A Simple Chess（Lucas + DP）

题目链接：http://acm.split.hdu.edu.cn/showproblem.php?pid=5794

题意：让一个棋子从（1,1）走到（n，m），要求像马一样走日字型并只能往右下角走。里面还有r个障碍点不能经过或者到达，问有多少种走法可以走到（n，m）。

思路：画个图可以发现走的点像一个斜着的杨辉三角。所以可以得到一个从点 i 走到点 j 的路径数是一个组合数。

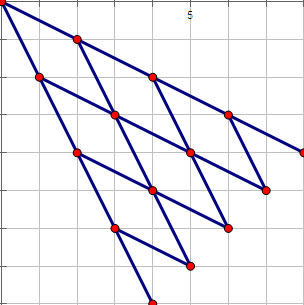大概就是长这样，杨辉三角的每个点的数如下。

1

1       1

1      2      1

1       3      3      1

1      4       6      4      1

1       5      10      10      5      1

1      6      15      20      15      6      1

1      7      21      35      35      21      7      1

找到规律：路径数为C（在这一步的位置，走过的步数）。走过的步数是当前的点 i 坐标（x，y），（x+y）/3就是步数了。当前的位置是min（x，y）-步数。这里的步数就相当于三角的层数。

首先对全部障碍从小到大进行排序，对于每个障碍 i，求出从（1，1）走到其的路径总数，减去之前的障碍（0 <= j < i）可以走到现在的障碍的路径总数（dp[i] -= dp[j] * 从点 j 走到点 i 的路径数）。组合数的计算要用到Lucas定理进行计算。

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <string>
 #include <cmath>
 #include <iostream>
 #include <stack>
 using namespace std;
 #define MOD 110119
 typedef long long LL;
 struct node
 {
     LL x, y;
 }p[];
 LL dp[];
 LL f[MOD+];
 /*
 dp[i]一开始表示从(0, 0)走到第i个点的路径数
 后面要减去如果前面有障碍,那么会有一部分路径是不能走的
 减去的路径数为分别为第j个点(0<=j<i)走到第i个点的路径数*dp[j]
 */

 bool cmp(const node &a, const node &b)
 {
     if(a.x == b.x) return a.y < b.y;
     return a.x < b.x;
 }

 void biao() //打出阶乘表
 {
     f[] = f[] = ;
     for(int i = ; i <= MOD; i++) {
         f[i] = f[i-] * i % MOD;
     }
 }

 LL quick_pow(LL a, LL b)
 {
     a %= MOD, b %= MOD;
     LL ans = ;
     while(b) {
         if(b & ) ans = ans * a % MOD;
         a = a * a % MOD;
         b >>= ;
     }
     return ans;
 }

 LL C(LL n, LL m)
 {
     if(m > n) return ;
     if(m < ) return ;
     LL ans = ;
     ans = ans * f[n] % MOD * quick_pow(f[m] * f[n-m] % MOD, MOD - ) % MOD;
     return ans;
 }

 LL Lucas(LL n, LL m)
 {
     if(m == ) return ;
     return C(n % MOD, m % MOD) % MOD * Lucas(n / MOD, m / MOD) % MOD;
 }

 int main()
 {
     LL n, m, r;
     int cas = ;
     biao();
     while(~scanf("%I64d%I64d%I64d", &n, &m, &r)) {
         memset(dp, , sizeof(dp));
         bool flag = ;
         for(int i = ; i < r; i++) {
             scanf("%I64d%I64d", &p[i].x, &p[i].y);
             if(p[i].x == n && p[i].y == m) flag = ;
             p[i].x--, p[i].y--;
         }
         sort(p, p + r, cmp);
         p[r].x = n - , p[r].y = m - ; //把目标点加入
         printf("Case #%d: ", ++cas);
         if(flag || (p[r].x + p[r].y) %  != ) { //如果障碍在目标点上或者不能走到目标点
             puts(""); continue;
         }
         for(int i = ; i <= r; i++) {
             if((p[i].x + p[i].y) %  == ) { //如果这个障碍是可以走到的
                 LL a = (p[i].x + p[i].y) / ; //第几层
                 LL b = min(p[i].x, p[i].y) - a; //位置
                 dp[i] = Lucas(a, b); //类似于杨辉三角的组合数
                 for(int j = ; j < i; j++) {
                     if(p[j].y >= p[i].y || p[j].x >= p[i].x) continue; //题目要求只能往右下角走
                     LL xx = (p[i].x - p[j].x);
                     LL yy = (p[i].y - p[j].y);
                     if((xx + yy) %  == ) { //要能够从j点走到i点
                         LL aa = (xx + yy) / ;
                         LL bb = min(xx, yy) - aa; //减去可以从j点走到i点的路径数
                         dp[i] -= (Lucas(aa, bb) * dp[j]) % MOD;
                         dp[i] = (dp[i] + MOD) % MOD;
                     }
                 }
             }
         }
         printf("%I64d\n", dp[r]);
     }
     return ;
 }