Stanford机器学习笔记-1.线性回归

Content：

1. Linear Regression

　　1.1 Linear Regression with one variable

　　　　1.1.1 Gradient descent algorithm

　　1.2 Linear Regression with multiple variable

　　　　1.2.1 Feature Scaling

　　　　1.2.2 Features and polynomial regression

　　　　1.2.3 Normal equation

　　　　1.2.4 Probalilistic interpretation for cost function

key words: Linear Regression, Gradient Descent, Learning Rate, Feature Scaling, Normal Equation

1. Linear Regression

1.1 Linear Regression with one variable

某个目标量可能由一个或多个变量决定，单变量线性回归就是我们仅考虑一个变量与目标量的关系。例如，我们可以仅考虑房子的面积X与房价y的关系，如下图。

通常将已有的可利用的数据成为data set or training set。

首先我们定义出线性的hypothesis function h，然后定义出cost function J，为了使得假设函数接近或等于实际值，目标是使得函数J取最小值。

1.1.1 Gradient descent algorithm (梯度下降法)

梯度下降法可以求解线性回归问题，具体描述如下：

函数J是一个二元函数，为使得取最小值，分别对求偏导数，得到对应的变化率。然后，设定一个合适的learning rate，对theta进行更新。更新策略如下：

注意更新要同步，否则前一个theta0会影响后一个theta1更新（通过影响cost function : J）

其中对J函数求偏导数如下：

带入得：

迭代次数和learning rate是影响梯度下降法是否成功收敛到最优值的重要因素。

迭代次数：
- 过少可能使得算法还没有收敛就停止，
- 过多导致资源（时间等）的浪费；
learning rate:
- 过小，使得每次迭代时theta的变化量过小，从而算法收敛过慢，换言之需要增加迭代次数使得算法收敛；
- 过大，使得每次迭代时theta的变化量过大，可能在变化（迭代）过程中越过最优（收敛）点。直观地：

正常的收敛应大致如下：

1.2 Linear Regression with multiple variables

在实际生活中，一个量通常受很多变量的影响。同样以房价为例：

此时相应的量（函数）有如下变化：theta从2维变成了n+1维向量；从而hypothesis function为下图所示（注意定义x0=1的小细节）:

同样的，可以用梯度下降法来解决多变量线性回归问题。

注意与单变量线性回归对应的变化和联系。事实上，单变量线性回归是多变量线性回归的特殊情况(n=1)。

1.2.1 Feature Scaling（数据规范化）

不同的特征量由于单位不同，可能在数值上相差较大，Feature Scaling可以去量纲，减少梯度下降法的迭代次数，提高速度，所以在算法执行前通常需要Feature Scaling。直观上来说，考虑两个特征量，规范化前的椭圆很瘪，可能导致收敛的路径变长，数据规范化后使得椭圆较均匀，缩短收敛路径，如下：

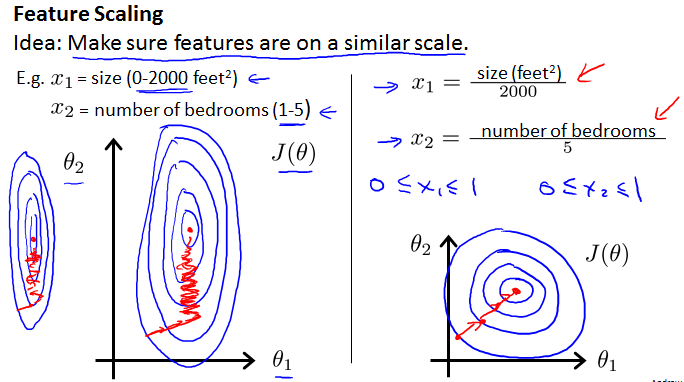
下面给出一种规范化策略:

求每个特征量X的平均值mean
求每个特征量X的标准差segma (matlab中std()函数)
规范化：X = (X-mean) / sigma

1.2.2 Features and polynomial regression

有时候，我们可以将某些特征量联合成一个新的特征量或许可以得到更好的结果，例如要预测房价，考虑到房价主要由area决定，不妨将特征量frontage和depth联合成一个新的特征量area.

对于有些情况，线性回归的结果可能不是很理想，可以考虑多项式回归。注意应该结合实际考虑选择几次的多项式，例如下面的例子，特征量是size，目标量是price，所以就不应该选择二次多项式，否则会出现size增大而price变小的情况，不符合实际情况。

1.2.3 Normal equation（正则方程）

Normal equation: Method to solve for analytically.

首先考虑cost function J的自变量theta为一维的情况，这时的J为关于theta的一元二次函数，可以直接求导得到最小值点，如下图所示:

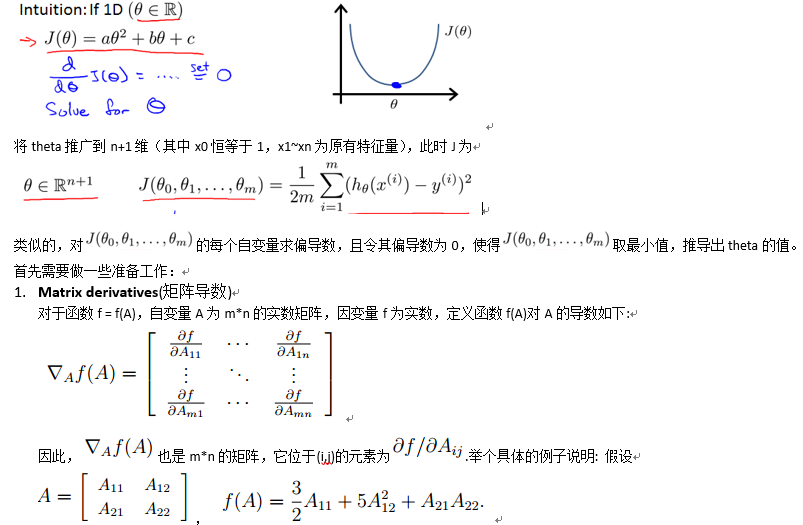
下面对Gradient Descent 和 Normal Equation做一下比较

m = 20000, n = 10000，优先考虑Gradient Descent
m = 20000, n = 10, 优先考虑Normal Equation

1.2.4 Probalilistic interpretation for cost function

参考：https://www.coursera.org/learn/machine-learning/