剑指offer第二版-10.斐波那契数列

面试题10：斐波那契数列

题目要求：
求斐波那契数列的第n项的值。f(0)=0, f(1)=1, f(n)=f(n-1)+f(n-2) n>1

思路：使用循环从下往上计算数列。

考点：考察对递归和循环的选择。使用递归的代码通常比循环简洁，但使用递归时要注意一下几点：1、函数调用的时间和空间消耗；2、递归中的重复计算；3、最严重的栈溢出。根据斐波那契数列递归形式定义很容易直接将代码写成递归，而这种方式有大量重复计算，效率很低。

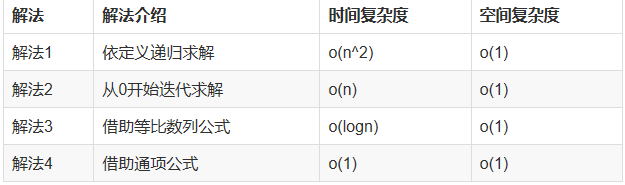
解法比较：
解法3,4将问题数学化，借助数学工具的推导，从根本上减低时间复杂度。

/**
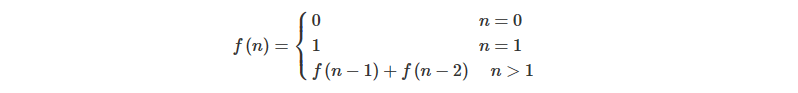
 * Copyright(C) 2019 Hangzhou Differsoft Co., Ltd. All rights reserved.
 *
 */
package com.java.offer;

/**
 * @since 2019年2月26日 下午12:59:43
 * @author xuchao
 *
 * 斐波那契数列 f(0)=0,f(1)=1,f(n)=f(n-1)+f(n-2) n>1
 */
public class P10_Fibonacci {
    // 1.依据原始概念的递归解法，时间复杂度o(n^2)
    public static int fibonacci1(int n) {
        if(n<=1) {
            return n;
        }
        return fibonacci1(n - 1) + fibonacci1(n - 2);
    }

    // 2.当前状态只与前两个状态有关。存储前两个值，计算后一个，迭代进行。时间复杂度o(n)
    public static int fibonacci2(int n) {
        if (n <= 1) {
            return n;
        }
        int f1 = 0;
        int f2 = 1;
        for (int i = 2; i <= n; i++) {
            int t = f1 + f2;
            f1 = f2;
            f2 = t;
        }
        return f2;
    }

    public static void main(String[] args) {
        System.out.println(fibonacci1(13));
        System.out.println(fibonacci1(13));
    }
}