深度搜索（dfs）+典型例题（八皇后）

深度优先搜索简称深搜，从起点出发，走过的点要做标记，发现有没走过的点，就随意挑一个往前走，走不了就回退，此种路径搜索策略就称为“深度优先搜索”，简称“深搜”。

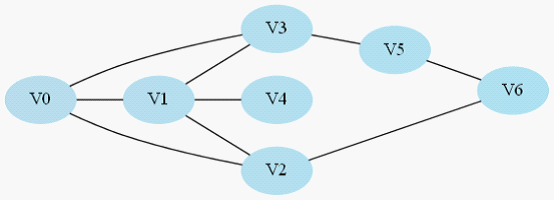
如上面的图所示：加入我们要找一个从V0到V6的一条最短的路径。我们可以看到有许多的路我们可以走。

V0——V3——V5——V6；

V0——V3——V1——V4；

V0——V3——V1——V2——V6；

V0——V1——V4；

V0——V1——V3——V5——V6；

V0——V1——V2——V6；

V0——V2——V6；

前两组，是从节点V3开始分的，然后遍历了后面的所有路径，然后找到了我们需要的解。

从第三条路径我们就可以看到，到了V4之后就没有路了，那么我们就需要返回到V1找下一条路径。

V1节点所有的路径我们就都找完了，就开始找V2节点的路径了。由于我们一开始不知道哪一条路可以走到V6和不知道哪一条路径最短，所以我们需要找出所有的路，然后再来判断哪一条路最短。

上面我们找到了所有的路径，然后判断最小的路径是V0——V2——V6，这就是最优解。

深搜的基本模板：

int search(int t)
{
    if(满足输出条件)
    {
        输出解;
    }
    else
    {
        for(int i=;i<=尝试方法数;i++)
            if(满足进一步搜索条件)
            {
                为进一步搜索所需要的状态打上标记;
                search(t+);
                恢复到打标记前的状态;//回溯
            }
    }
}

总结：深搜就是要找到所有可能的解，然后再来找到最优解，需要我们遍历所有的路径。

典型例题（八皇后）：链接：https://www.luogu.org/problem/P1219

题目描述

检查一个如下的6 x 6的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。

上面的布局可以用序列2 4 6 1 3 5来描述，第i个数字表示在第i行的相应位置有一个棋子，如下：

行号 1 2 3 4 5 6

列号 2 4 6 1 3 5

这只是跳棋放置的一个解。请编一个程序找出所有跳棋放置的解。并把它们以上面的序列方法输出。解按字典顺序排列。请输出前3个解。最后一行是解的总个数。

输入格式

一个数字N (6 <= N <= 13) 表示棋盘是N x N大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例

输入 #1复制

6

输出 #1复制

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

对于该题目，因为我们不知道怎样来放这个点，所以我们需要将所有的点都试一下，防止漏掉哪一个点：

题解：

#include<iostream>
using namespace std;
int sum=;
int A[]={},B[]={},C[]={},D[]={};//表示横行，B表示纵行，C表示左下到右上的对角线，D表示左上到右下的对角线
int n;
int print()//输出前三个
{

    if(sum<=)
    {
        for(int i=;i<=n;i++)
         cout<<A[i]<<" ";
         cout<<endl;
    }
    sum++;
 }
 void dfs(int i)
 {
      if(i>n)
      {
          print();
          return ;
       }
     if(i<=n)
     {
         for(int j=;j<=n;j++)
         {
             if(B[j]!=&&C[j-i+n]!=&&D[i+j]!=)
             {
                 A[i]=j;//记录纵列的值
                 B[j]=;//标记纵列
                 C[j-i+n]=;//标记对角线
                 D[i+j]=;//标记对角线
                 dfs(i+);//接着搜下一个点
                 B[j]=;//清除记忆
                 C[j-i+n]=;
                 D[j+i]=;
             }
         }
     }
 }
 int main()
 {
     cin>>n;
     dfs();
     cout<<sum-;
     return ;
 }