hdu 1978 How many ways（dp）

Problem Description

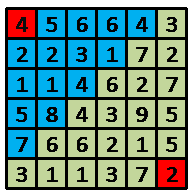这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下： 1.机器人一开始在棋盘的起始点并有起始点所标有的能量。 2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。 3.机器人不能在原地停留。 4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)
点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。 我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

 

Input

第一行输入一个整数T,表示数据的组数。 对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。

 

Output

对于每一组数据输出方式总数对10000取模的结果.

 

Sample Input

1
6 6
4 5 6 6 4 3
2 2 3 1 7 2
1 1 4 6 2 7
5 8 4 3 9 5
7 6 6 2 1 5
3 1 1 3 7 2

 

Sample Output

3948

 

方法一：当前的这个点可以到达其他点的方法数（直接4重循环）

 #pragma comment(linker, "/STACK:1024000000,1024000000")
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<math.h>
 #include<algorithm>
 #include<queue>
 #include<set>
 #include<bitset>
 #include<map>
 #include<vector>
 #include<stdlib.h>
 using namespace std;
 #define ll long long
 #define eps 1e-10
 #define MOD 10000
 #define inf 1e12
 #define N 106
 int n,m;
 int mp[N][N];
 int dp[N][N];
 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--){
         scanf("%d%d",&n,&m);
         for(int i=;i<=n;i++){
             for(int j=;j<=m;j++){
                 scanf("%d",&mp[i][j]);
             }
         }
         memset(dp,,sizeof(dp));
         dp[][]=;
         for(int i=;i<=n;i++){
             for(int j=;j<=m;j++){
                 for(int k=i;(k<=n) && (k<=mp[i][j]+i);k++){
                     for(int w=j;(w<=m) && (w<=mp[i][j]+i+j-k);w++){
                         if((k==i) && (w==j))continue;
                         dp[k][w]+=dp[i][j];
                         dp[k][w]%=MOD;
                     }
                 }
             }
         }
         printf("%d\n",dp[n][m]%MOD);
     }
     return ;
 }

方法二：记忆化dp，标记dp[n][m]=1,然后从前往后记忆化dp，dfs

 #pragma comment(linker, "/STACK:1024000000,1024000000")
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<math.h>
 #include<algorithm>
 #include<queue>
 #include<set>
 #include<bitset>
 #include<map>
 #include<vector>
 #include<stdlib.h>
 using namespace std;
 #define ll long long
 #define eps 1e-10
 #define MOD 10000
 #define N 106
 #define inf 1e12
 int n,m;
 int mp[N][N];
 int dp[N][N];
 bool judge(int x,int y){
     if(x< || x>n || y< || y>m) return false;
     return true;
 }
 int dfs(int x,int y){
     if(dp[x][y]>=) return dp[x][y];
     dp[x][y]=;
     for(int i=;i<=mp[x][y];i++){
         for(int j=;j<=mp[x][y]-i;j++){
             if(judge(x+i,y+j)){
                dp[x][y]=(dp[x][y]+dfs(x+i,y+j))%MOD;
             }
         }
     }
     return dp[x][y];
 }
 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--){
         scanf("%d%d",&n,&m);
         for(int i=;i<=n;i++){
             for(int j=;j<=m;j++){
                 scanf("%d",&mp[i][j]);
             }
         }
         memset(dp,-,sizeof(dp));
         dp[n][m]=;
         printf("%d\n",dfs(,));
     }
     return ;
 }