back propogation 的线代描述

参考资料：

　　算法部分：

　　　　standfor, ufldl  : http://ufldl.stanford.edu/wiki/index.php/UFLDL_Tutorial

　　　　一文弄懂BP：https://www.cnblogs.com/charlotte77/p/5629865.html

　　代码部分：

　　　　siraj raval ，4分钟搭建神经网络: http://192.168.73.134/www.sohu.com/a/162305418_697750

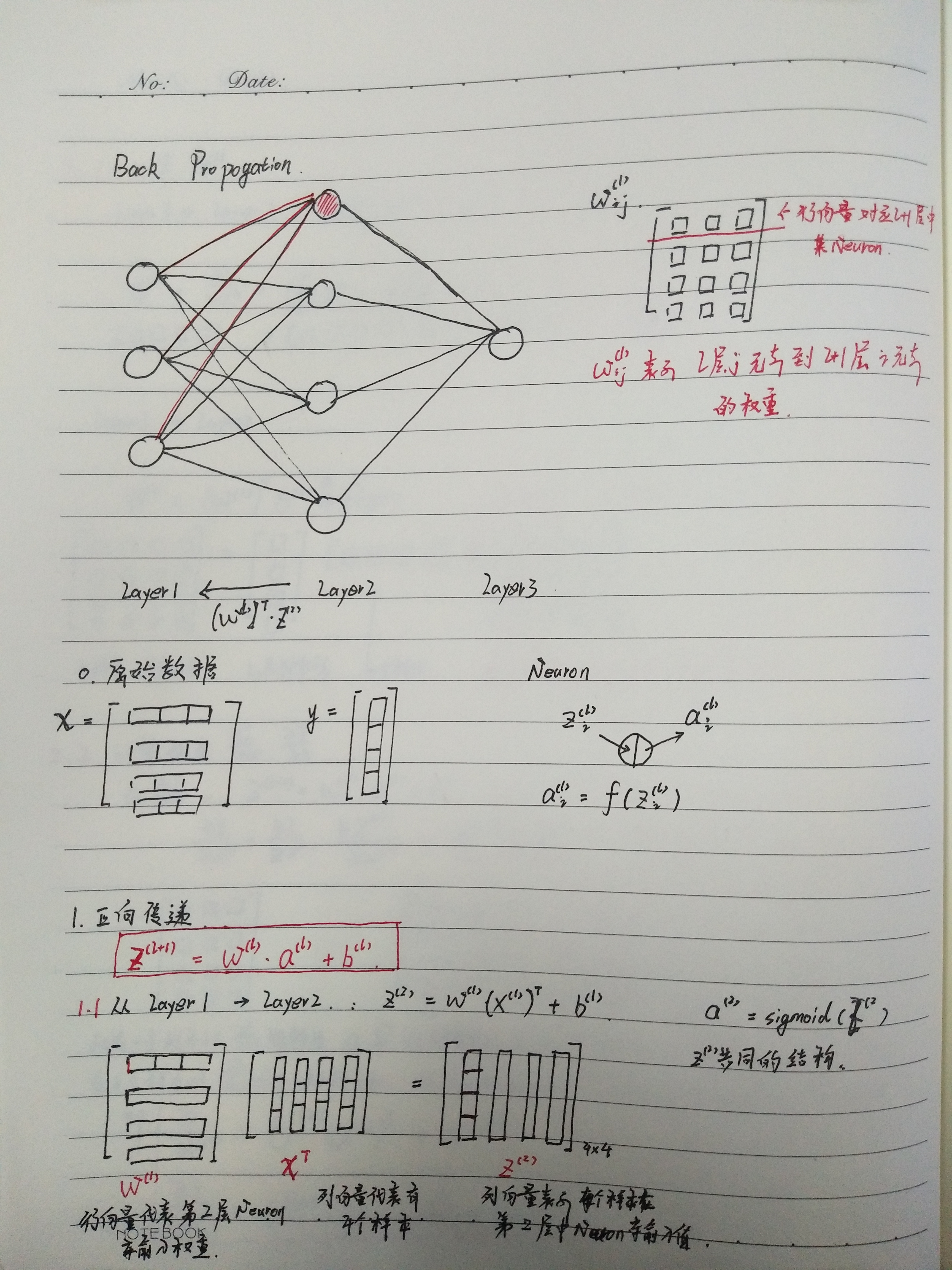
　　这是我个人学习笔记，希望其他阅读者已经学习过 ufldl关于 neural network 和 back propogation的内容。

最重要的就是 求解梯度更新公式的矩阵形式（笔记中红框中部分）：

python 代码，numpy 实现：

# -*- coding=utf-8 -*-

import numpy as np
r'''
    build a neural network by plain numpy
    loss (latex)
        J(w,b) = \frac{1}{m} \sum_{i}^{m}\frac{1}{2}\left \| h_{wb}(x^{(i)}) - y^{(i)} \right \|^2 +\sum \sum \sum W^{(l)}_{(ij)}

'''
def getData():
    x = np.array([[0, 0, 1], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
    y = np.array([0, 1, 1, 0])[:, np.newaxis]
    return x, y

def sigmoid(x, deriv=False):
    if deriv is True:
        fx = sigmoid(x)
        return fx * (1.0 - fx)
    else:
        return 1.0 / (1.0 + np.exp(-x))

x, y = getData()
fy = sigmoid(y)
# print(fy)
# np.random.seed(30)
w1 = np.random.random([4, 3])
b1 = np.random.random([4, 1])
w2 = np.random.random([1, 4])
b2 = np.random.random([1, 1])

max_iter = 100000
nita = 0.0  # regular
step_size = 0.1

for i in range(0, max_iter):
    # forward
    z2 = np.dot(w1, x.T) + b1  # 4×4+4×1 (broadcasting)
    a2 = sigmoid(z2)
    z3 = np.dot(w2, a2) + b2[0, 0]
    y_hat = sigmoid(z3)

    # mse
    mse = (1.0 / y.shape[0]) * np.dot((y.T - y_hat).T, y.T - y_hat)[0, 0]
    if i % 500 == 0 or mse < 0.0001:
        print('when i=' + str(i) + '; mse:' + str(mse))
        if mse < 0.0001:
            break
    # backward
        # partial
    delta_3 = (y_hat - y.T) * sigmoid(z3, deriv=True)
    delta_2 = np.dot(w2.T, delta_3) * sigmoid(z2, deriv=True)

    partial_w2 = np.dot(delta_3, a2.T) + nita * w2
    partial_b2 = np.dot(delta_3, np.ones([4, 1]))
    partial_w1 = np.dot(delta_2, x) + nita * w1
    partial_b1 = np.dot(delta_2, np.ones([4, 1]))

        # update parameter
    w2 -= step_size * partial_w2
    b2 -= step_size * partial_b2
    w1 -= step_size * partial_w1
    b1 -= step_size * partial_b1

print(y_hat)