Elasticsearch集成HanLP分词器-个人学习

1、通过git下载分词器代码。

连接如下：https://gitee.com/hualongdata/hanlp-ext

hanlp官网如下：http://hanlp.linrunsoft.com/

2、下载gradle,如果本机有，就可以略过此步骤。通过gradle官方网站下载，解压，配置环境即可。

官方安装配置说明：https://gradle.org/install/

3、按本地elasticsearch进行打包。

注意：通过git下载的源代码，除非与git配置的版本相同，否则可能会导致你elasticearch无法加载分词器。

修改git下载的源代码包中的elasticsearch版本。并通过gradle进行打包。会自动下载同步elasticsearch对应版本的jar包。

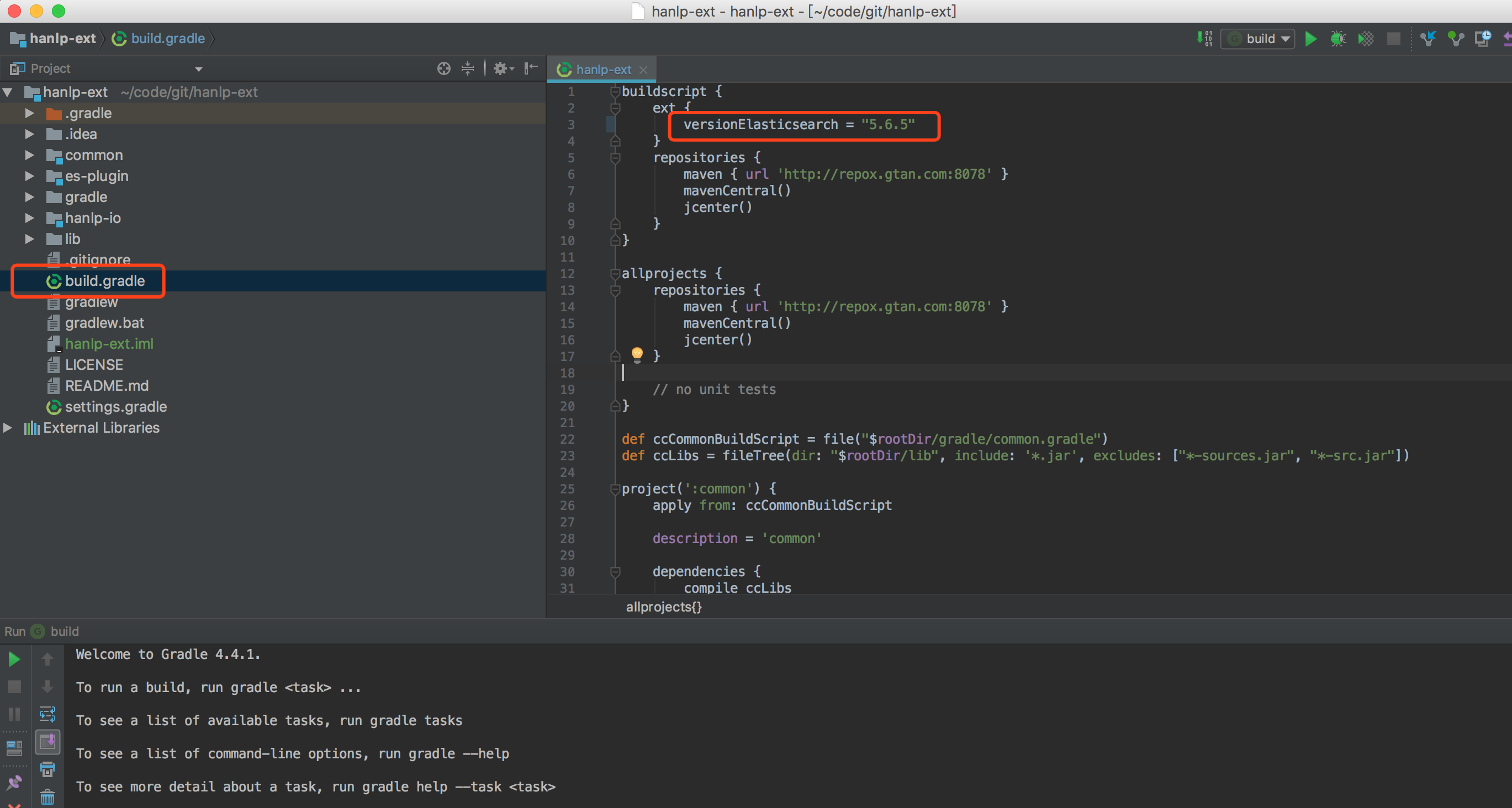
4、按本地环境配置词类位置

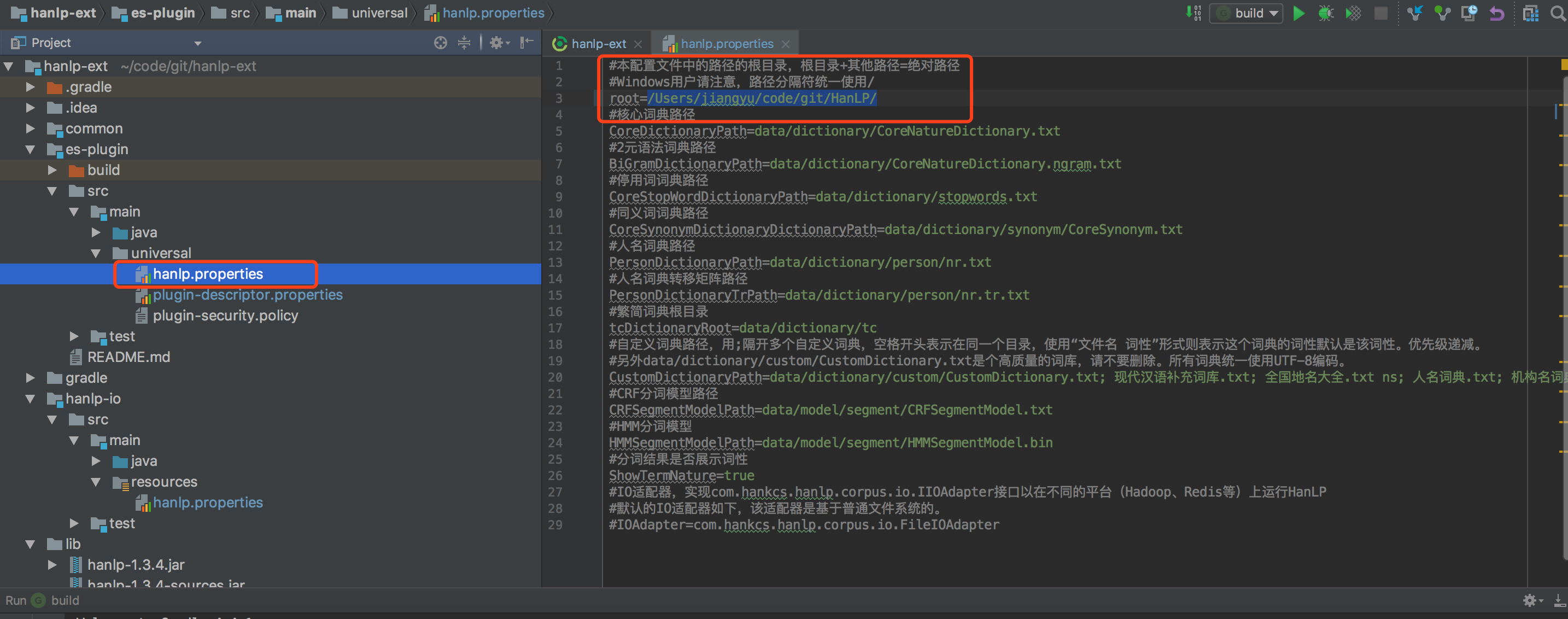
5、配置打包的插件所对应支持的elasticesarch的版本。(修改为：5.6.5，es安装的学习环境为5.6.5)

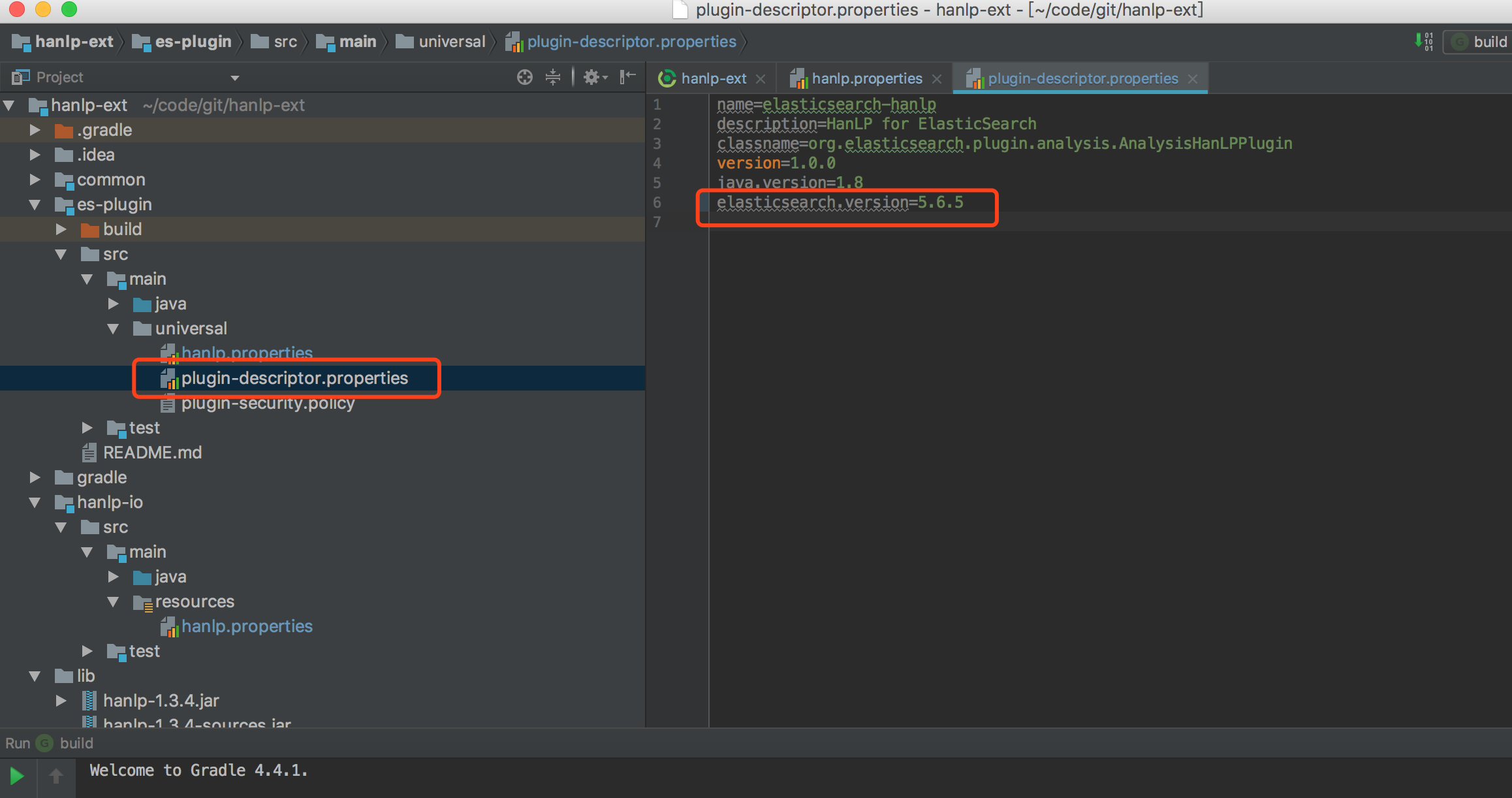
6、完成上述配置把。gradle自动下载对应版本的包。可以通过如下方式进行版本查看。

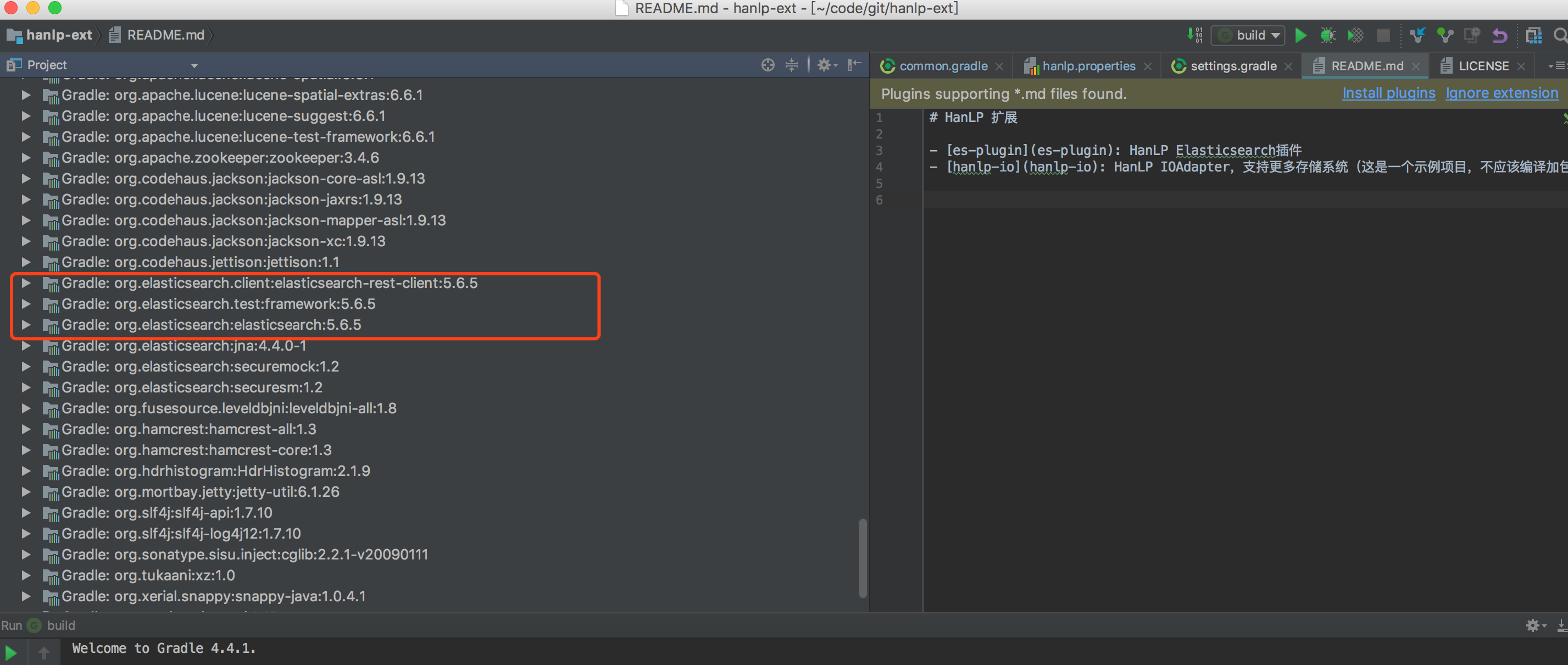
7、确认对应版本的包存在后，在工程所在目录下执行如下命令进行打包：

gradle -p es-plugin jar buildPluginZip

如下操作：在项目工程目录下，运行命令。

8、打包完成后，会出现对应的安装包。

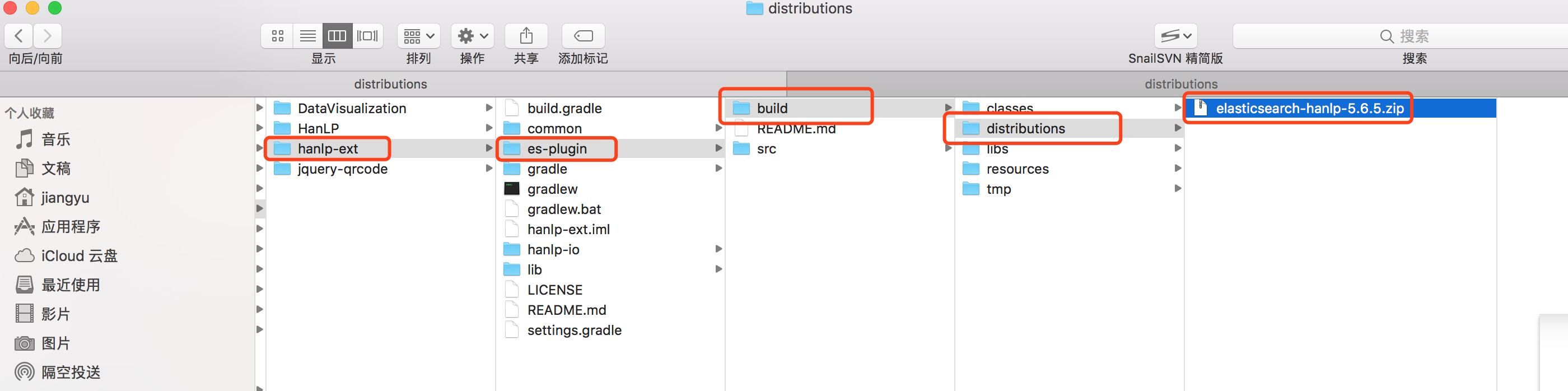
9、在elasticsearch安装目录下执行插件安装命令。

./bin/elasticsearch-plugin install file:///Users/jiangyu/code/git/hanlp-ext/es-plugin/build/distributions/elasticsearch-hanlp-5.6.5.zip

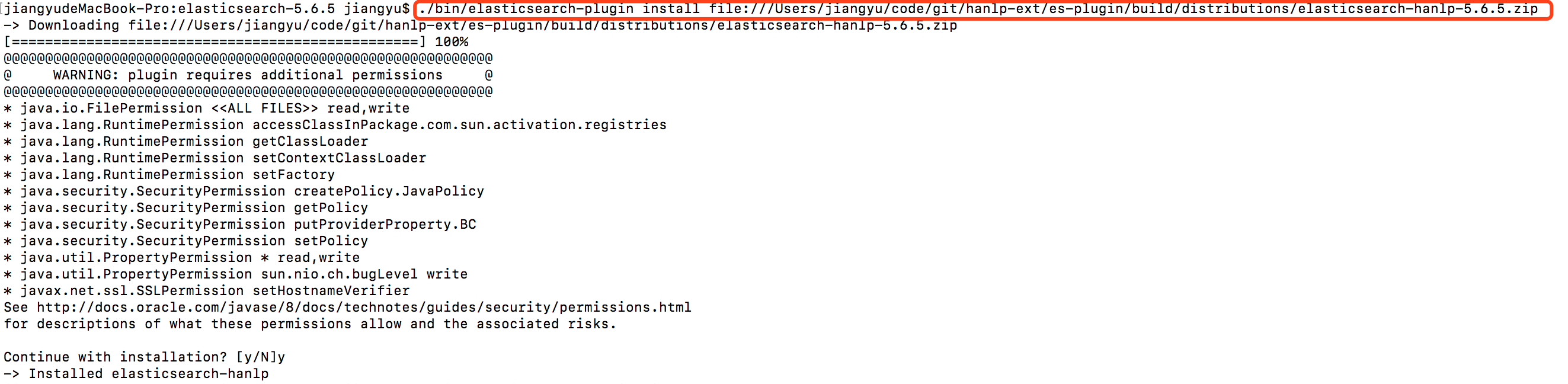
可以看到上面安装完成的提示。有个过程要选择y。

注：如果上向的命令出现如下报错。错误提示如下:

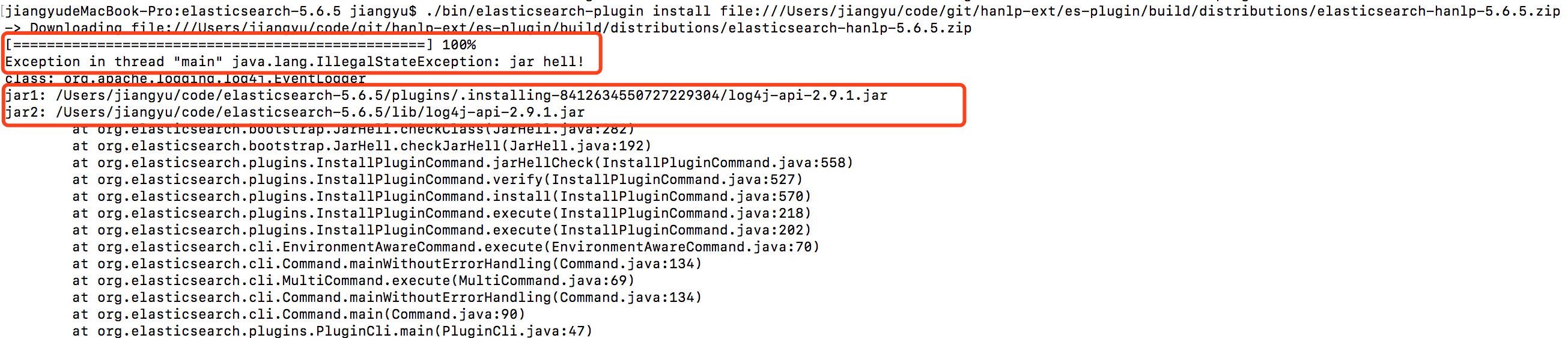
上述错误提示，说明有两个相同的jar包存在。所以有提示，可以先在build.gradle配置中，找到打包的过程，增加一条path.contains("org.apache.logging.log4j")配置，这样打包时，这个jar包不会在被找到插件中。配置修改完成后。从新执行第7步『gradle -p es-plugin jar buildPluginZip』，进重新打包。再重新安装插件即可。

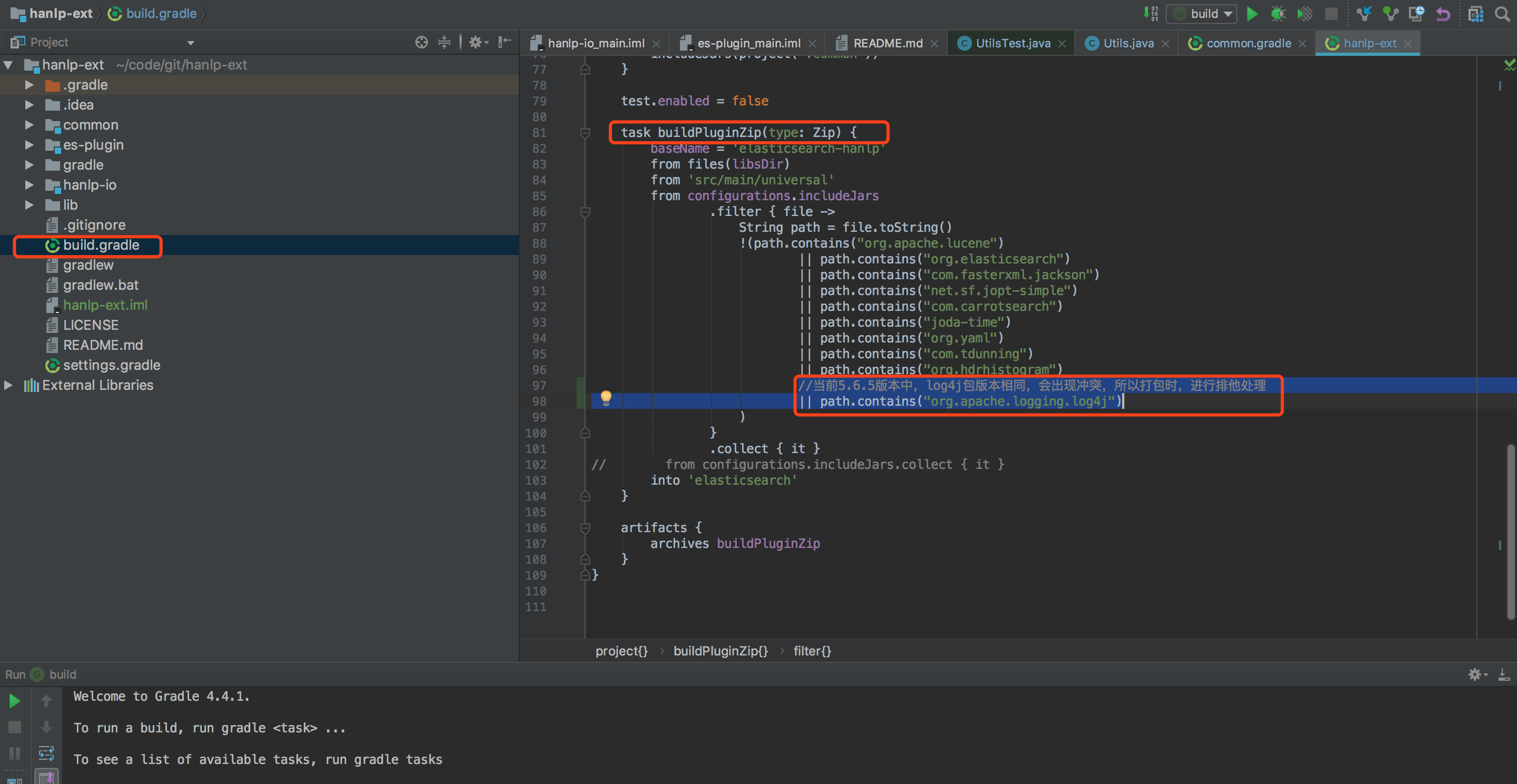
（注：测试时，这个包不能去掉。会导致测试插件时，缺少log4j包）

10、给插件增加访问权限

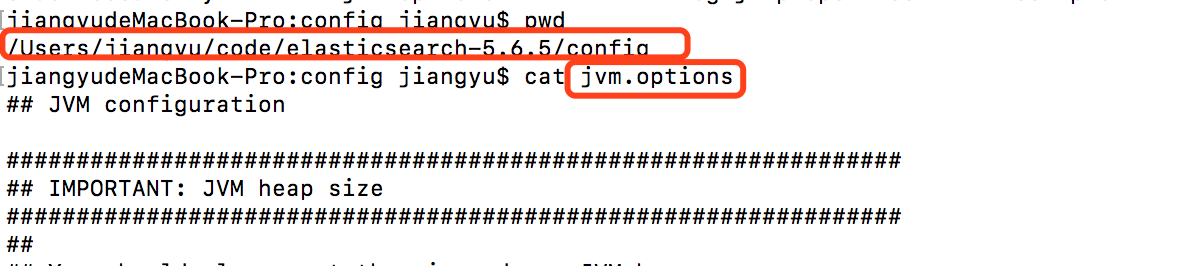
在系统的elasticsearch的安装目录下，找到config目录，通过vi jvm.options打开文件进行编辑。增加如下内容：用来指定安全配置文件。

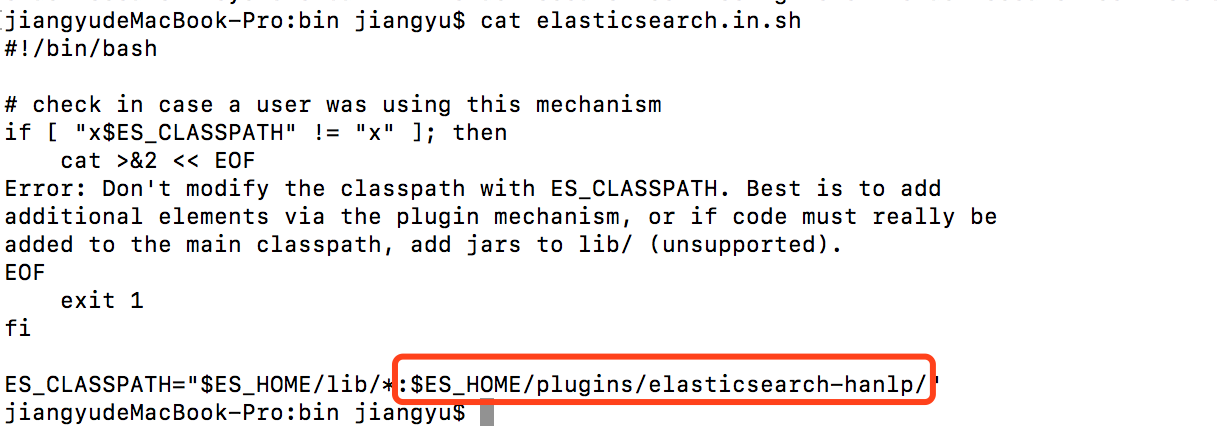
11、修改elasticsearch配置，在系统的elasticsearch的安装目录下，找到bin目录，通过vi elasticearch.in.sh打开文件进行编辑。增加如下内容：用来指定安全配置文件。

在文件中增加指定的lib包。我们将插件要用到的Lib包路径引入到系统环境变量中。

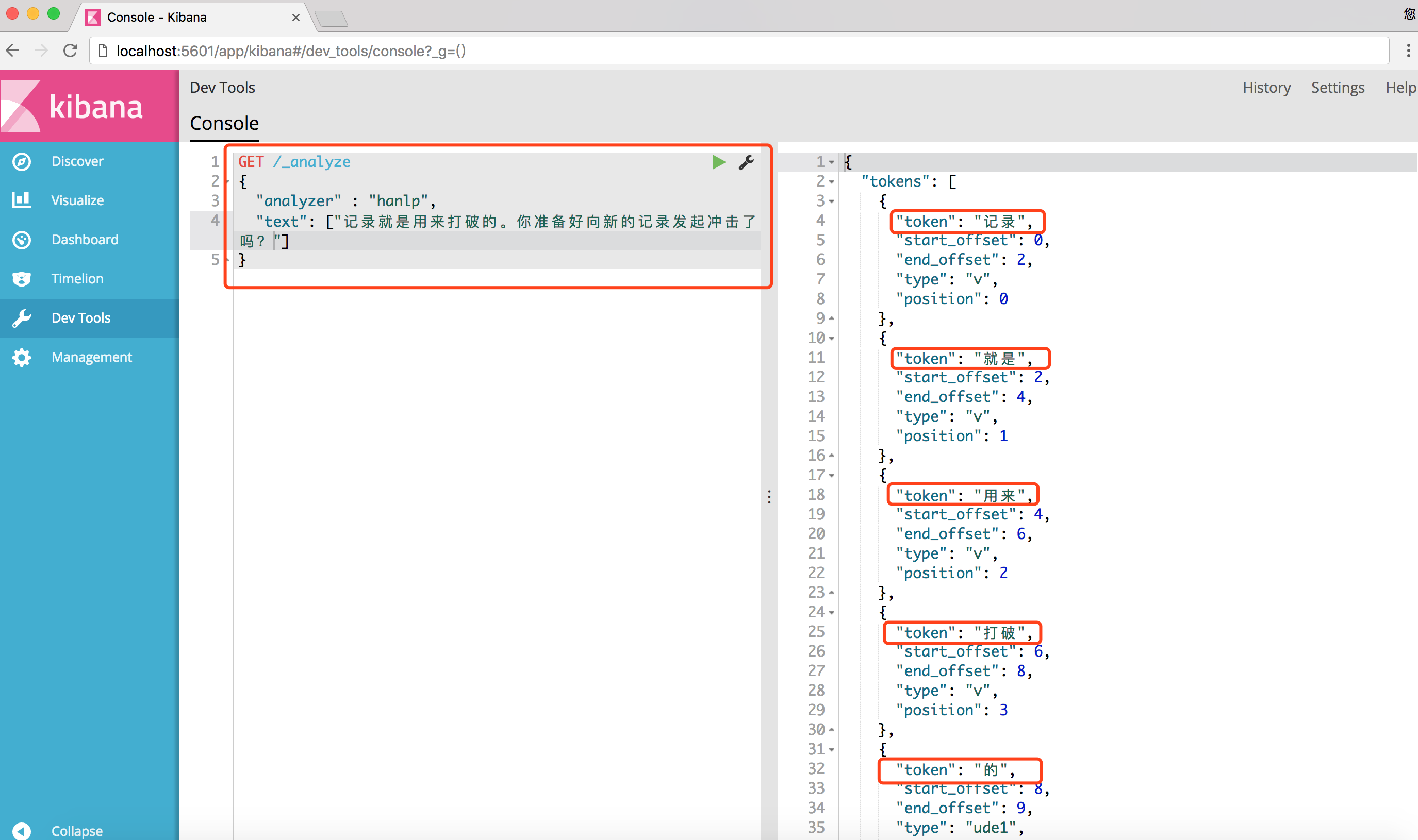
14、安装完成后可以使用如下命令进行验证。 analyzer,指定分词器为："hanlp"

GET /_analyze

{

"analyzer" : "hanlp",

"text": ["记录就是用来打破的。你准备好向新的记录发起冲击了吗？"]

}

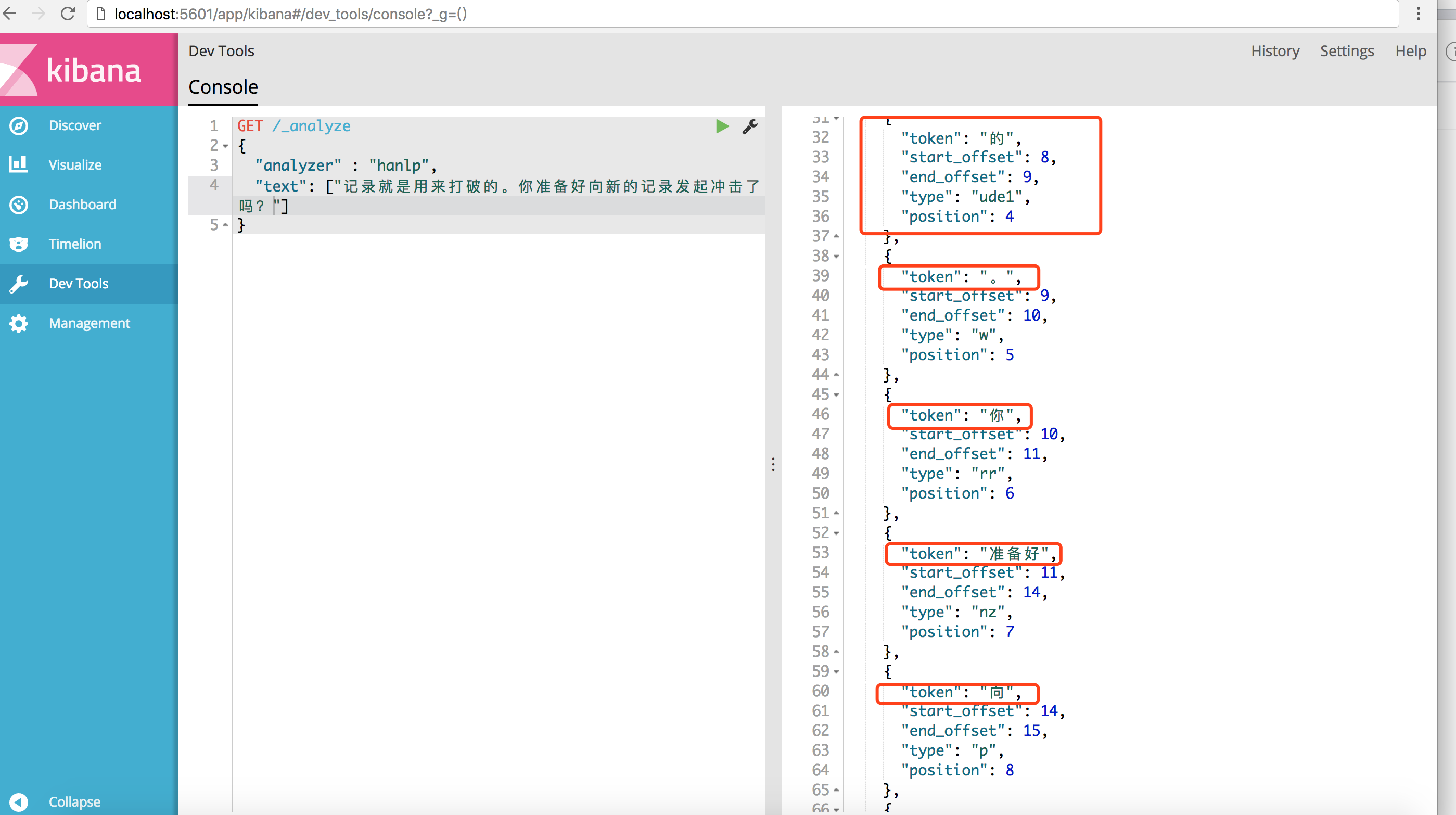
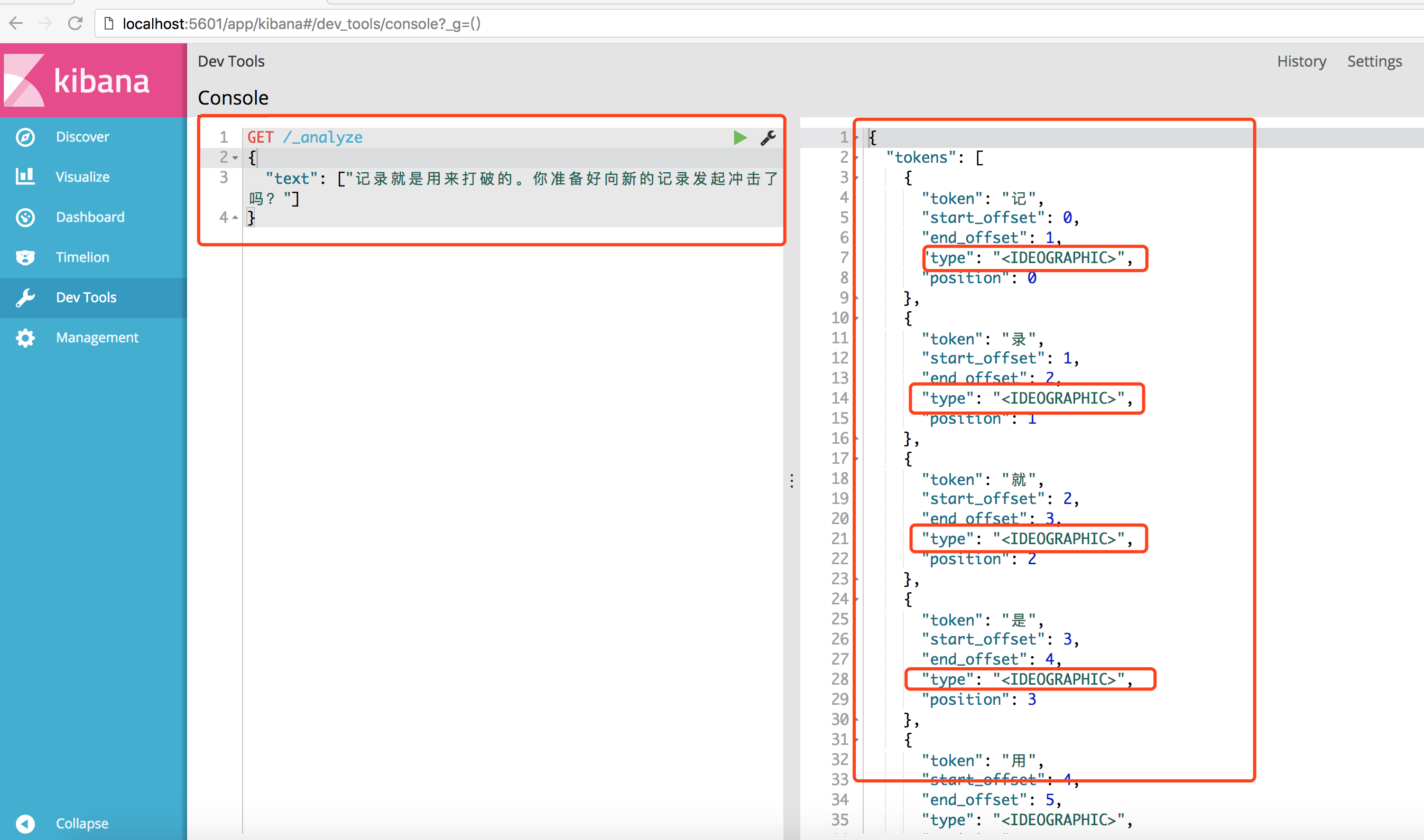
如果不指定分词器的话。所以返回结果，type没有说明词性，都是按单字返回结果。

GET /_analyze

{

"text": ["记录就是用来打破的。你准备好向新的记录发起冲击了吗？"]

}

参考连接如下：https://gitee.com/hualongdata/hanlp-ext/tree/master/es-plugin、

其它操作：

1、如果想移除或删除插件，可以执行如下命令

来源：https://my.oschina.net/u/3519280/blog/1621783