深入理解Adaboost算法

理解算法确实是欲速则不达，唯有一步一步慢慢看懂，然后突然觉得写的真的太好了，那才是真的有所理解了。

Adaboost的两点关键点：

1. 如何根据弱模型的表现更新训练集的权重；

2. 如何根据弱模型的表现决定弱模型的话语权

算法步骤：

从训练数据中训练出一系列的弱分类器，然后把这些弱分类器集成为一个强分类器，这里并没有继续对强分类器继续合成。

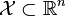给定一个训练数据集T={(x1,y1), (x2,y2)…(xN,yN)}，其中实例，而实例空间，yi属于标记集合{-1,+1}，Adaboost的目的就是从训练数据中学习一系列弱分类器或基本分类器，然后将这些弱分类器组合成一个强分类器。

Adaboost的算法流程如下：

• 步骤1. 首先，初始化训练数据的权值分布。每一个训练样本最开始时都被赋予相同的权值：1/N。

• 步骤2. 进行多轮迭代，用m = 1,2, ..., M表示迭代的第多少轮

a. 使用具有权值分布Dm的训练数据集学习，得到基本分类器（选取让误差率最低的阈值来设计基本分类器）：

b. 计算Gm(x)在训练数据集上的分类误差率

由上述式子可知，Gm(x)在训练数据集上的误差率em就是被Gm(x)误分类样本的权值之和。

c. 计算Gm(x)的系数，am表示Gm(x)在最终分类器中的重要程度（目的：得到基本分类器在最终分类器中所占的权重）：

由上述式子可知，em <= 1/2时，am >= 0，且am随着em的减小而增大，意味着分类误差率越小的基本分类器在最终分类器中的作用越大。

d. 更新训练数据集的权值分布（目的：得到样本的新的权值分布），用于下一轮迭代

使得被基本分类器Gm(x)误分类样本的权值增大，而被正确分类样本的权值减小。就这样，通过这样的方式，AdaBoost方法能“重点关注”或“聚焦于”那些较难分的样本上。

其中，Zm是规范化因子，使得Dm+1成为一个概率分布：

• 步骤3. 组合各个弱分类器

从而得到最终分类器，如下：