解答：

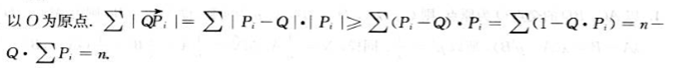
评：最小值在Q为球心时取到，体现数学对称性的美！

MT【1】终点在球面上的向量的更多相关文章

  1. python 库 Numpy 中如何求取向量范数 np.linalg.norm(求范数)（向量的第二范数为传统意义上的向量长度），（如何求取向量的单位向量）

    求取向量二范数,并求取单位向量(行向量计算) import numpy as np x=np.array([[0, 3, 4], [2, 6, 4]]) y=np.linalg.norm(x, axi ...

  2. UVA10827球面上的最大和

    题意:      最大子矩阵的加强版,就是给你一个n*n的矩阵,每个格子里面都有数字,然后我们在里面选择一个矩阵,使得矩阵中所有数字的和最大,而且这个题目说这个n*n的矩阵的最右边和最左边是相邻的,最 ...

  3. 【转载】屏幕坐标向3维坐标的转化-DXUT的CD3DArcBall类

    原文:http://blog.csdn.net/bluekitty/article/details/6070828 3D应用程序中,我们可以通过鼠标进行空间中物体的旋转和视角的变换等,而鼠标的移动是2 ...

  4. 3D数学读书笔记——向量运算及在c++上的实现

     本系列文章由birdlove1987编写.转载请注明出处.     文章链接: http://blog.csdn.net/zhurui_idea/article/details/24782661   ...

  5. 线性代数的本质与几何意义 01. 向量是什么？(3blue1brown 咪博士 图文注解版)

    向量是线性代数最基础.最基本的概念之一,要深入理解线性代数的本质,首先就要搞清楚向量到底是什么? 向量之所以让人迷糊,是因为我们在物理.数学,以及计算机等许多地方都见过它,但又没有彻底弄懂,以至于似是 ...

  6. OpenGL 用三角形模拟生成球面

    在看OpenGL红皮书,看到生成球体这节,讲了很多,总感觉不如自己动手写一些代码来的实在,用OpenGL中三角形模拟球形生成.主要要点,模型视图变换,多边形表面环绕一致性,矩阵堆栈.先贴上代码. 虽然 ...

  7. 向量的表示及协方差矩阵 （PCA的理论基础）

    原文:http://blog.csdn.net/songzitea/article/details/18219237 引言 当面对的数据被抽象为一组向量,那么有必要研究一些向量的数学性质.而这些数学性 ...

  8. [BZOJ4311]向量(凸包+三分+线段树分治)

    可以发现答案一定在所有向量终点形成的上凸壳上,于是在上凸壳上三分即可. 对于删除操作,相当于每个向量有一个作用区间,线段树分治即可.$O(n\log^2 n)$ 同时可以发现,当询问按斜率排序后,每个 ...

  9. PCA算法详解——本质上就是投影后使得数据尽可能分散（方差最大），PCA可以被定义为数据在低维线性空间上的正交投影，这个线性空间被称为主⼦空间（principal subspace），使得投影数据的⽅差被最⼤化（Hotelling, 1933），即最大方差理论。

    PCA PCA(Principal Component Analysis,主成分分析)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量 ...

随机推荐

  1. 你想要的Python面试都在这里了【315+道题】

    写在前面 近日恰逢学生临近毕业,课程后期大家"期待+苦逼"的时刻莫过于每天早上内容回顾和面试题问答部分[临近毕业每天课前用40-60分钟对之前内容回顾.提问和补充,专挑班里不爱说话 ...

  2. 5个python爬虫教材，让小白也有爬虫可写，含视频教程！

    认识爬虫   网络爬虫,如果互联网是一张蜘蛛网,网络爬虫既是一个在此网上爬行的蜘蛛,爬了多少路程即获取到多少数据. python写爬虫的优势   其实以上功能很多语言和工具都能做,但是用python爬 ...

  3. LVDS接口分类，时序，输出格式

    LVDS接口分类,时序,输出格式 2016年01月19日 16:57:35 打个飞机去美国 阅读数:24673 标签: LVDS液晶屏格式时序 更多 个人分类: 硬件基础   1.1.1        ...

  4. Python学习总结 05 pandas

     pandas官方网址 : http://pandas.pydata.org/ . pandas的安装比较复杂,如果想开箱即用,可以考虑下载WinPython.WinPython的官方地址是: htt ...

  5. BugkuCTF web基础$_GET

    前言 写了这么久的web题,算是把它基础部分都刷完了一遍,以下的几天将持续更新BugkuCTF WEB部分的题解,为了不影响阅读,所以每道题的题解都以单独一篇文章的形式发表,感谢大家一直以来的支持和理 ...

  6. SKINNY加密算法详解(无代码，仅加密)

    原作者论文请参考<The SKINNY Family of Block Ciphers and Its Low-Latency Variant MANTIS> 地址为:https://li ...

  7. HTTP 及相关知识

    什么是HTTP.流程? 什么是AJAX.方法.状态码?

  8. oracle数据库添加新用户

    /*分为四步 */ /*第1步:创建临时表空间 */ create temporary tablespace kmyf_temp tempfile 'E:\app\pangxy\product\11. ...

  9. 第三个sprint冲刺第二阶段

    内测版:

  10. 使用matlab自带工具实现rcnn

    平台:matlab2016b matlab自带一个cifar10Net工具可用于深度学习. 图片标注 这里使用的是matlab自带的工具trainingImageLabeler对图像进行roi的标注. ...