Matlab_xcorr_互相关函数的讨论

假设两个平稳信号 $\textbf{x}$ 和 $\textbf{y}$ ，如果 $x\left(t+\tau\right)= y\left(t\right)$ ，则可通过互相关求 $\tau$ 。由于信号处理相关知识都蘸酱吃了，理论相关的部分咱们来日方长（我一定可能会补充的）。

XCORR 实现

---

首先，通过实现 xcorr 函数介绍互相关计算流程：

clc
clear
close

%  实现 xcorr 函数

% 基本设置
T = 1;              % [s] 总时间长度
fs = 5000;          % [Hz] 采样频率
t = 0:1/fs:T;       % [s] 时间坐标
N = length(t);      % 信号个数

% 信号生成
tm = [ t(1:N) - T , t(2:N) ];       % 相关结果的时间延迟坐标轴
td1 = 0.2*T;                        % x 信号时间延迟
td2 = 0.3*T;                        % y 信号时间延迟
noise = rand(1,2*N);                % 生成了两倍时间 T 长度的噪声 [0,1]噪声
x = noise(1+round(td1*fs):N+round(td1*fs))-0.5*ones(1,N);
y = noise(1+round(td2*fs):N+round(td2*fs))-0.5*ones(1,N);

% 求取互相关
z1 = xcorr(x,y);　　　　 % Matlab 自带函数
[~,I1] = max(abs(z1));　% 模仿 Matlab doc 给出延迟坐标
z2 = zeros(1,N);　　　　 % 自编函数
for n = 1:length(tm)
    z2(n) = sum( x( max(1,n-N+1):min(n,N) ).*y( max(1,N-n+1):min(2*N-n,N) ) );
end
[~,I2] = max(abs(z2));　% 模仿 Matlab doc 给出延迟坐标
%---------------------计算说明--------------------%
% case1：               | case2:                 %
%              .N       |              .2*N-n    %
% y:  ..........        | y:       ..........    %
%           .N-n+1      |          .1            %
%              .n       |              .N        %
% x:        ..........  | x:  ..........         %
%           .1          |          .n-N+1        %
%------------------------------------------------%
err = z1-z2;        % 两种算法的差

% 绘图
subplot(1,3,1)
    plot(tm,z1)
    title('Matlab function')
    xlabel('time delay')
    ylabel('Amp')
    a1 = gca;
    a1.XTick = sort([-1:0.5:1 tm(I1)]);
subplot(1,3,2)
    plot(tm,z2)
    title('My function')
    xlabel('time delay')
    ylabel('Amp')
    a2 = gca;
    a2.XTick = sort([-1:0.5:1 tm(I2)]);
subplot(1,3,3)
    plot(tm,err,'.-')
    title('error')
    xlabel('time delay')
    ylabel('Amp')
suptitle('xcorr realization') 

以上 Matlab 代码可以得到下面的结果。从左到右依次是 Matlab 自带函数、我编的互相关函数、两个函数的差值。不难发现：两个函数十分接近，但是差值不为零。个人猜测是因为 xcorr 的求和和 sum 求和的截断误差不同所致。这个误差的来源我懒得去编程序验证了——毕竟10^-16量级的差别，没多大深究的意义。但是可以注意到这个差值有四个特点：

　　 - 小幅值时有固定几个数值

　　 - 每跑一次程序，rand 产生的噪声数据不同，error 值不同

　　 - 呈“纺锤型”，中间高，两边低

　　 - 实际值大的数据点，error 值大

最后要谈一下 xcorr 的噪声问题。我们通常使用的噪声是白噪声，或者高斯白，有一个很重要的特点就是均值为零，也就是说没有直流分量。但是当我们的噪声存在直流分量的时候（比如上面的噪声信号直接使用rand(1,2*N)时），互相关就是一个类似等腰三角形的东西了（想想门函数卷积）。回忆一下，对于存在稳定周期分量的两组信号 $\textbf{x}$ 、 $\textbf{y}$ 而言，互相关结果将会是一个幅度为“纺锤形”的周期震荡的信号。由此可观：互相关一方面可以得到非周期信号延迟结果，同时也能反映极端情况下，相同频率成分的存在，这一点可以用来观察工频干扰程度。

XCORR 与 CONV

---

互相关 xcorr 与 conv 的差别在于两点：

　　 - xcorr 在两段信号较短者后补零，使两段信号长度一致

　　 - xcorr 直接用两个信号的各种延迟做相乘求和，conv 使用翻褶后的信号做相乘求和

　　　　这导致了：

　　　　　　 1、xcorr(x,y) 中 (x,y) 顺序有影响，而conv(x,y) 没有

　　　　　　 2、两者在大部分情况下得到的结果是不一样的，但是对于一些有趣的对称信号是存在等价关系的。有兴趣的读者可以搞一搞，找找规律。因为本人并不搞对称相关的研究，这点就不展开了。下面的例子是有等价关系的。

clc
clear
close

%  比较 conv xcorr

% 例子　　
A = ones(1,12);　　% -3:3
B = 0:4;　　　　　　% 3:-1:-3
C = xcorr(A,B);
D = conv(A,B);

%绘图
subplot(2,2,1)
    plot(A,'.-')
    ylim([ -0.1 5.1 ])
    xlim([ 0.9 12.1])
    title('A = ones(1,12)')
    xlabel('n')
    ylabel('Amp')
subplot(2,2,2)
    plot(B,'.-')
    ylim([ -0.1 5.1 ])
    xlim([ 0.9 12.1])
    title('B = 0:4')
    xlabel('n')
    ylabel('Amp')
subplot(2,2,3)
    plot(C,'.-')
    ylim([ -0.1 15.1 ])
    xlim([ 0.9 25.1])
    title('xcorr 结果')
    xlabel('n')
    ylabel('Amp')
subplot(2,2,4)
    plot(D,'.-')
    ylim([ -0.1 15.1 ])
    xlim([ 0.9 25.1])
    title('cone 结果')
    xlabel('n')
    ylabel('Amp')
suptitle('conv与xcorr对比')

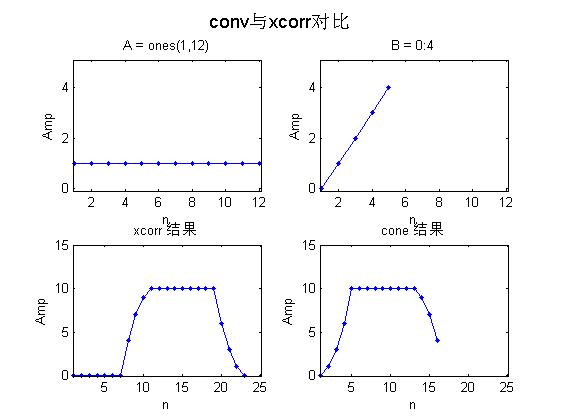
有兴趣的读者可以试着用给定函数实现目标函数：

　　 - xcorr --> fliplr

　　 - xcorr --> conv

　　 - conv --> fliplr

　　 - conv --> xcorr

---

END