图像特征与描述子（直方图， 聚类， 边缘检测， 兴趣点/关键点， Harris角点， 斑点（Blob), SIFI, 纹理特征）

1.直方图

用于计算图片特征，表达， 使得数据具有总结性， 颜色直方图对数据空间进行量化，好比10个bin

2. 聚类

类内对象的相关性高

类间对象的相关性差

常用算法：kmeans， EM算法， meanshift， 谱聚类（密度聚类）， 层次聚类

kmeans聚类

选取k个类中心，随机选取

计算每个点跟k个类中心的位置

把数据点分配给距离最近的一个类中心

计算新的类中心-对该类中的所有点取均值

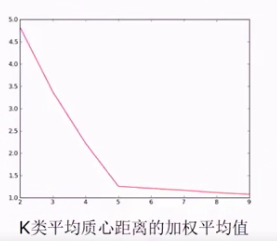
类中心数K的选取

K类平均质心的距离加权平均值， 当k=5时的斜率发生变化，我们可以选取5作为分类的个数

kmeans ++ 半随机（初始点的选取）

第一类中心 - 随机选取

记D（x） 为数据点x距离最近的聚类中心的距离

选取下一个聚类中心， 选取的概率正比于D(x) ^ 2

以此类推，到第k个

量化颜色直方图

聚类颜色直方图： 使用聚类算法对像素点颜色向量进行聚类， 单元由聚类中心代表

3. 边缘检测

像素明显变化的区域， 具有丰富的语义信息

用途： 物体识别，几何视角变化

定义： 像素函数快速变化的区域， 一阶导数的极值区域，二阶导数的0点位置

步骤：

先高斯去噪，再使用一阶导数获取极值

公式：        对x方向进行求导  б 表示的是标准差                                                    对y方向进行求导

梯度幅值/强度

hx（x，y）^ 2 + hy(x, y) ^ 2

梯度（增加最快）方向

arctan（hy（x, y）/ hx（x, y）)

4. 兴趣点/关键点

稳定局部

特点： 可重复性，显著性

抗图片变化

外貌变化（亮度，光照）

几何变化（平移， 选择，尺度）

5.Harris角点

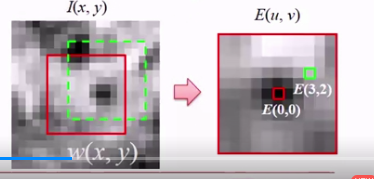
一种显著点：在任何方向上移动小观察窗，导致大的像素变动

　　Ｅ(u, v) =  ΣW(x, y)[I(x+u, y+v)-I(x, y)] ^2

W(x, y)是高斯函数进行加权的， x，y表示当前位置， u和v表示移动了的位置

6.斑点（Blob）

拉普拉斯梯度：一阶导数极值点 - 二阶导数零点

梯度/边缘可以通过查找：二阶导数接近零， 一阶导数足够大

对噪声很敏感， 需要先做高斯平滑

公式： Δf = δ2f / δ2x +  δ2f / δ2y 对x求二阶导， 对y方向求二阶导

斑点是找拉普拉斯的极值

边缘是找拉普拉斯的零值

7.SIFT

SIFT特征计算

计算高斯差分（DoG）尺度空间，获取极值点

特征点处理： 位置插值， 去除低对比度点， 去除边缘点

方向估计： 2*2网格， 8个方向，获得最高值为关键点的主方向，特征点方向归一化，即所有方向为同一方向

描述子提取: 在旋转坐标上采样16*16的像素窗， 4*4网格，8方向直方图，总共178维

8.纹理特征

HOG（方向梯度直方图）

梯度幅值，方向 s = sqrt（sx^2 + sy^2）

Block 拆分

16*16的block 步长是8， 包含2*2个cell， 每个cell8*8， 9个方向

积累梯度幅值，使用位置高斯加权，使用相邻bin线性插值

64&128的维度图：7*15 * （2*2） * 9 = 3780

LBP(局部二值模式)

将每个像素点与周围点大小半径比较，半径R的圆上，均匀采样P个点，根据赫值大小，量化为0或1