BZOJ 4808 马 二分图最大独立集

题目应该就是最大独立集了吧，没什么了，平面图求最大独立集需要/2的，

WQH说加直接+双向边考研过，结果真的过了，应该是匈牙利算法寻找的

时候更加快了吧。（方便找边）

 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<iostream>
 #include<cstring>
 #define N 207
 using namespace std;

 const int lx[]={,,,,-,-,-,-};
 const int ly[]={,,-,-,-,-,,};

 int n,m;
 int a[N][N],mark[N][N],du[N*N];
 int cnt,head[N*N],next[N*N*N],rea[N*N*N];
 int dui[N*N],flag[N*N];

 void add(int u,int v){next[++cnt]=head[u],head[u]=cnt,rea[cnt]=v;}
 bool dfs(int u)
 {
     for (int i=head[u];i!=-;i=next[i])
     {
         int v=rea[i];
         if (flag[v]) continue;
         flag[v]=;
         if (!dui[v]||dfs(dui[v]))
         {
             dui[v]=u;
             return ;
         }
     }
     return ;
 }
 int main()
 {
     memset(head,-,sizeof(head));
     scanf("%d%d",&n,&m);
     int num=;
     for (int i=;i<=n;i++)
         for (int j=;j<=m;j++)
         {
             scanf("%d",&a[i][j]);
             mark[i][j]=(i-)*m+j;
             if (a[i][j]) num++;
         }
     int x,y;
     for (int i=;i<=n;i++)
         for (int j=;j<=m;j++)
             if (a[i][j]==)
                 for (int k=;k<;k++)
                 {
                     x=i+lx[k],y=j+ly[k];
                     if(a[x][y]) continue;
                     if (x<=n&&x>=&&y>=&&y<=m) add(mark[i][j],mark[x][y]),add(mark[x][y],mark[i][j]);
                 }
     memset(dui,,sizeof(dui));
     int ans=;
     for (int i=;i<=n;i++)
         for (int j=;j<=m;j++)
             if (a[i][j]==)
             {
                 memset(flag,,sizeof(flag));
                 ans+=dfs(mark[i][j]);
             }
     ans=n*m-num-ans/;
     printf("%d",ans);
 }

其实还有更优秀的思想

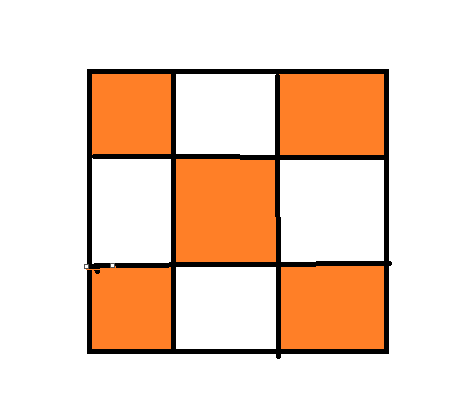（图太丑，不管了）

这里可以，将平面图分成这样的格点图，玩过国际象棋的都知道，马是一黑一白交替着走的，

也就说，在同种颜色中，马不会相互攻击，那只需要计算一种颜色中最大独立集就可以了，

这样就是先记录可以填的位置，然后只需要操作一种颜色，连边出去，连向另外一个集合，

这样匹配的就是无法共存点，这样就OK了。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 #define hash(A,B) ((A)*m-m+B)
 #define ok(A,B) (A>=1&&A<=n&&B>=1&&B<=m&&!mp[A][B])
 #define N 40010
 #define M 500010

 int m,n,flow,sum;
 int cnt,head[N],vis[N],match[N],mp[][];
 struct Edge{int to,nxt;}e[M];
 int dis[][]={{-,},{-,-},{,},{,-},{-,},{-,-},{,},{,-}};

 void adde(int u,int v)
 {
     e[++cnt].to=v;
     e[cnt].nxt=head[u];
     head[u]=cnt;
 }
 bool dfs(int u,int flag)
 {
     for(int i=head[u];~i;i=e[i].nxt)
     {
         int v=e[i].to;
         if(vis[v]==flag) continue;
         vis[v]=flag;
         if(!match[v]||dfs(match[v],flag))
         {
             match[v]=u;
             return ;
         }
     }
     return ;
 }
 int main()
 {
     cnt=;sum=;flow=;
     memset(head,-,sizeof(head));
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;++i)
     for(int j=;j<=m;++j) scanf("%d",&mp[i][j]);
     for(int i=;i<=n;++i)
     for(int j=;j<=m;++j)
     {
         if(mp[i][j]) continue;sum++;
         if((i^j)&)
         {
             for(int k=;k<;++k)
             if(ok(i+dis[k][],j+dis[k][]))
             {
                 adde(hash(i,j),hash(i+dis[k][],j+dis[k][]));
             }
         }
     }
     for(int i=;i<=n;++i)
     for(int j=;j<=m;++j)
     {
         if(mp[i][j]) continue;
         if((i^j)&)
         {
             int p=hash(i,j);
             if(dfs(p,p)) flow++;
         }
     }
     printf("%d\n",sum-flow);
     return ;
 }