poj 1390 Blocks (记忆化搜索)

Blocks

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 4318		Accepted: 1745

Description

Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold. 

The corresponding picture will be as shown below: 

 

Figure 1


If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1
box(es) in the segments respectively. 



Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points. 



Now let's look at the picture below: 

 

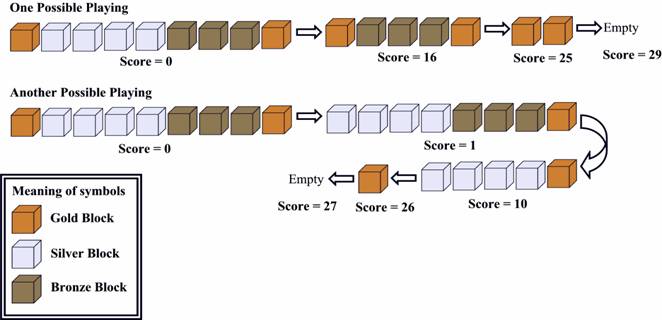
Figure 2




The first one is OPTIMAL. 



Find the highest score you can get, given an initial state of this game. 

Input

The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range
1~n.

Output

For each test case, print the case number and the highest possible score.

Sample Input

2
9
1 2 2 2 2 3 3 3 1
1
1

Sample Output

Case 1: 29
Case 2: 1

递归形式的动态规划：dp[st][ed][len]从st到ed全然消除。且ed右边挨着有一个len的大块颜色和ed同样.

一种消除方式是，Len块直接和ed块合并直接消除得到分数work（st,ed-1,0）+（a[ed].n+len）*(a[ed].n+len);

还有一种是在st到ed之间找到一个块p和ed块颜色同样，把这3块直接合并 work（st,p，a[ed].n+len）+work(p+1,ed-1,0);

两种方式取最大的值。

当st==ed时递归结束。

#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
#include<queue>
using namespace std;
#define LL __int64
#define N 210
const int inf=0x1f1f1f1f;
struct node
{
    int c,n,p;
}a[N];
int f[N][N][N];
int work(int st,int ed,int len)
{
    if(f[st][ed][len])
        return f[st][ed][len];
    int i,ans=(a[ed].n+len)*(a[ed].n+len);
    if(st==ed)
    {
        f[st][ed][len]=ans;
        return ans;
    }
    ans+=work(st,ed-1,0);
    for(i=ed-1;i>=st;i--)
    {
        if(a[i].c!=a[ed].c)
            continue;
        int tmp=work(st,i,a[ed].n+len)+work(i+1,ed-1,0);
        if(tmp<=ans)
            continue;
        ans=tmp;
        break;
    }
    f[st][ed][len]=ans;
    return ans;
}

int main()
{
    int T,t,cnt,i,n,Cas=1;
    scanf("%d",&T);
    while(T--)
    {
        memset(a,0,sizeof(a));
        scanf("%d",&n);
        scanf("%d",&t);
        cnt=0;
        a[cnt].c=t;
        a[cnt].n=1;
        for(i=1;i<n;i++)
        {
            scanf("%d",&t);
            if(t==a[cnt].c)
            {
                a[cnt].n++;
            }
            else
            {
                cnt++;
                a[cnt].c=t;
                a[cnt].n=1;
            }
        }
        memset(f,0,sizeof(f));
        printf("Case %d: %d\n",Cas++,work(0,cnt,0));
    }
    return 0;
}