LeetCode笔记：39. Combination Sum

题目描述

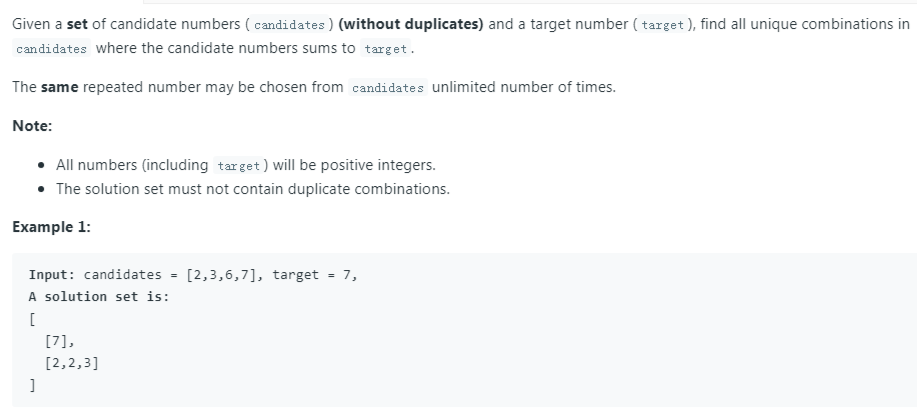
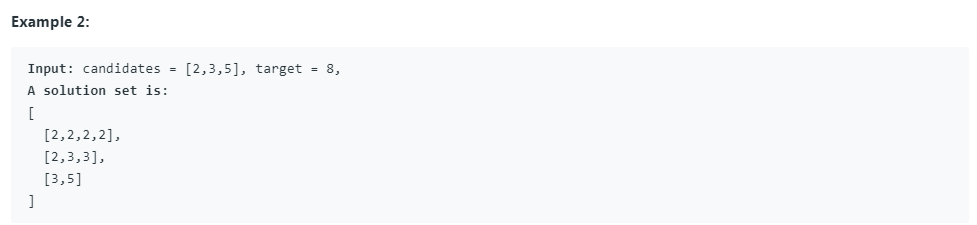
给定一个无重复的正整数数组 candidates 和一个正整数 target， 求所有和为 target 的 candidates 中数的组合中。其中相同数的不同顺序组合算做同一种组合，candidates 中的数可以重复使用。

算法一

首先想到的方法就是枚举所有的组合可能性，判断其和是否为target。枚举的方法可以使用递归，对candidates中每一个数，有“加入组合”和“不加入组合”两种选择，每一种选择又可以向后面元素的不同选择递归，直到candidate中最后一个元素。可以用剪枝来减少算法的运行时间，如果当前组合的和大于target，则当前情形下已不会有合适的组合了。

AC代码如下：

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        dfs(candidates, 0, target, new ArrayList<Integer>(), res);
        return res;
    }

    private void dfs(int[] candidates, int index, int target, List<Integer> combination, List<List<Integer>> res) {
         if(target < 0) return;
        if(target == 0) {
            res.add(new ArrayList<>(combination));
            return;
        }

        for(int i=index; i<candidates.length; i++) {
            if(candidates[i] > target) continue;
            //选择当前元素
            combination.add(candidates[i]);
            dfs(candidates, i, target - candidates[i], combination, res);
            //不选择当前元素
            combination.remove(combination.size() - 1);
        }
    }
}

算法二

本题符合动态规划的思想，用一个map记录不同target的全部组合，target <=  0的组合为空, target = i的组合为全部 target = i - candidates[j] (0<j<candidates.length)的组合加上candidates[j]。

这里需要注意，因为题目要求相同元素的不同顺序算同一种组合方式，上诉方法会出现[2,3,2] 和 [2,2,3]这样两种组合方式。可以用将每一种组合排序后加入set的方法来去重。

AC代码：

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Map<Integer, List<List<Integer>>> dp = new HashMap<Integer, List<List<Integer>>>();
        return dp(target, 0, candidates, dp);
    }

    private List<List<Integer>> dp(int target, int index, int[] candidates, Map<Integer, List<List<Integer>>> map){
         if(map.containsKey(target)) {
            return map.get(target);
        }

        List<List<Integer>> resList = new ArrayList<>();
        Set<List<Integer>> resSet = new HashSet<>();

//这里一定要能够区分出 小于0和等于0.       等于0时加一个空的，避免出现[2，3,6,7] ，target = 7时，6被放入其中！！！！
        if(target < 0 ) return resList;
        if(target == 0){
            resList.add(new ArrayList<>());
            return resList;
        }

        for(int i=index; i<candidates.length; i++){
            List<List<Integer>> subResList = dp(target - candidates[i], index, candidates, map);
            if(subResList.size() > 0) {
                for(List<Integer> subRes : subResList) {
                    List<Integer> res = new ArrayList<>(subRes);
                    res.add(candidates[i]);
                    Collections.sort(res);
                    resSet.add(res);
                }
            }
        }
        for(List<Integer> l : resSet) {
            resList.add(l);
        }

        map.put(target, resList);
        return resList;
    }
}

算法三

本题还可以采用背包问题的思想，target相当于背包的容量，candidates为物品。

用一个map记录sum的范围从0~target的所有组合，容量为 i 的组合求解方式如下：遍历每一个物品candidates[j]， 获取容量为 i - candidates[j]的所有组合，加入该物品。

这里值得注意的是，因为题目要求相同元素的不同顺序算同一种组合方式，因此需要将物品的循环放在容量循环的外面，这样就可以避免出现重复出现[2,3,2] 和 [2,2,3]这样两种组合方式。

AC代码：

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Map<Integer, List<List<Integer>>> m = new HashMap<>();
        m.put(0, new ArrayList<List<Integer>>());

        for(int i=0; i<candidates.length; i++){
            for(int j=0; j<=target; j++){
                if(j < candidates[i]) continue;
                List<List<Integer>> l = m.get(j - candidates[i]);
                if(l != null) {
                    List<List<Integer>> jList = m.getOrDefault(j, new ArrayList<List<Integer>>());
                    if(l.size() == 0){
                        List<Integer> lcurr = new ArrayList<>();
                        lcurr.add(candidates[i]);
                        jList.add(lcurr);
                    }else{
                        for(List<Integer> listInL : l){
                            List<Integer> lcurr = new ArrayList<>(listInL);
                            lcurr.add(candidates[i]);
                            jList.add(lcurr);
                        }
                    }
                    m.put(j, jList);
                }
            }
        }
        return m.getOrDefault(target, new ArrayList<List<Integer>>());
    }
}