[总结]最小生成树之Kruskal算法

目录

• 一、最小生成树的相关知识
  • 1. 树的性质
  • 2. 生成树
  • 3. 最小生成树
  • 4. 最小生成树的性质
• 二、Kruskal算法求最小生成树
  • 1. 核心思想
  • 2. 具体流程
  • 3. 图示
  • 4. 代码实施
• 三、例题
  • 例1：P2212 [USACO14MAR]浇地Watering the Fields
  • 例2：P1550 [USACO08OCT]打井Watering Hole
  • 例3：P1547 Out of Hay
  • 例4：P1340 兽径管理

---

一、最小生成树的相关知识

1. 树的性质

树实际上是图的特殊形态，

对于任意一张无向连通图\(G=(V,E)\)，其中\(n=|V|，m=|E|\)。

该图为树时的性质：

1. |E|=|V|-1
2. 图中无环
3. 图连通
4. 任意两点有且仅有一条简单路径
5. 删除任意一条边后该图不连通

2. 生成树

在一个有\(|V|\)个点的无向连通图中，取其中\(|V|-1\)条边，并连接所有的顶点，所得到的子图为原图的生成树(Spanning Tree)。

3. 最小生成树

在一个带权无向连通图中，各边权和最小的一棵生成树即为原图的最小生成树(Minimum Spanning Tree，MST)。

4. 最小生成树的性质

1. 最小边原则：图中权值最小的边(唯一)一定在最小生成树上。

2.唯一性定理：对于一个图\(G\)，如果图中边权都不相同，那么该图的最小生成树唯一(形态不一定唯一)。

---

二、Kruskal算法求最小生成树

求出一个图的最小生成树共有两种算法：Prim算法，Kruskal算法。

由于Prim算法的实用性较低，因此这里不介绍该算法。

1. 核心思想

Kruskal算法是一种贪心思想，将边权按权值由小到大排序，并从剩下的边集中选择权值最小且两个端点不在同一集合的边加入生成树中，重复该操作直到加入了\(n-1\)条边。

2. 具体流程

1. 将边权由小到大排序。
2. 建立并查集，每个点都构成一个集合。
3. 扫描每一条边(x,y,z)，若发现x,y在同一集合，那么舍弃这条边；否则累计z到答案中并合并x,y到同一集合。
4. 重复操作3直到生成树中包含n-1条边。若所有边扫描完毕且生成树的边数不到n-1，那么该图不存在最小生成树。

总时间复杂度为：\(O(mlogm+m\alpha (n))\)，其中\(\alpha (n)\)是一次并查集的复杂度。

3. 图示

以下组图具体描述了Step：0中的一个图求出最小生成树的过程。

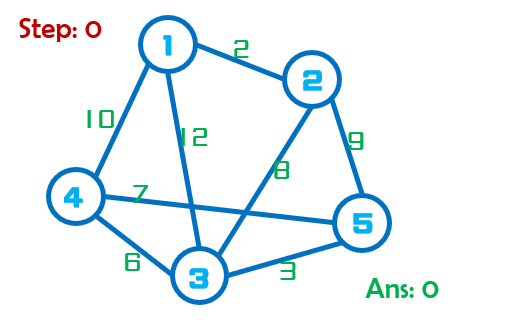
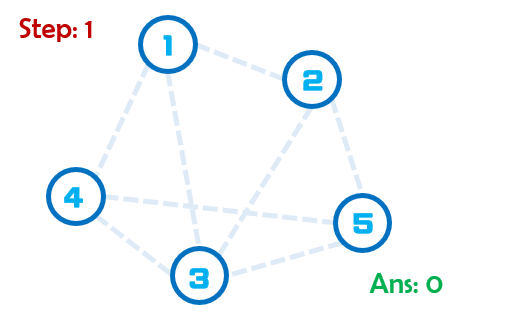
Step：1初始每个点都是一个集合。

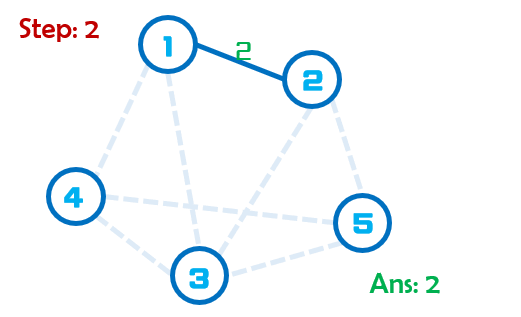
Step：2当前最小边权为2，因此将点1,2合并到同一个集合。

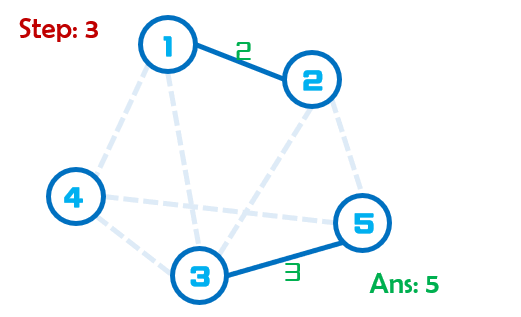
Step：3当前最小边权为3，因此将点3,5合并到同一个集合。

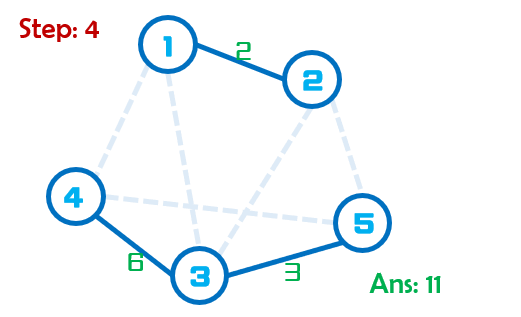
Step：4当前最小边权为6，点3,4不在同一集合，因此将点3,4合并到同一个集合。

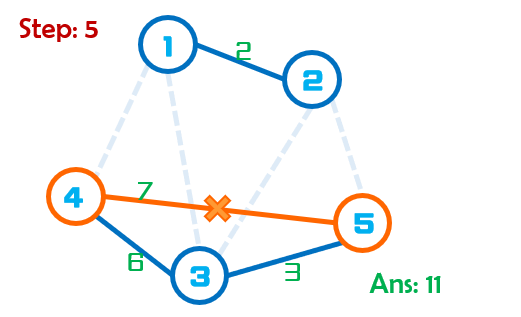
Step：5当前最小边权为7，由于此时点4,5已经在同一集合，因此将点3,4合并到同一个集合。

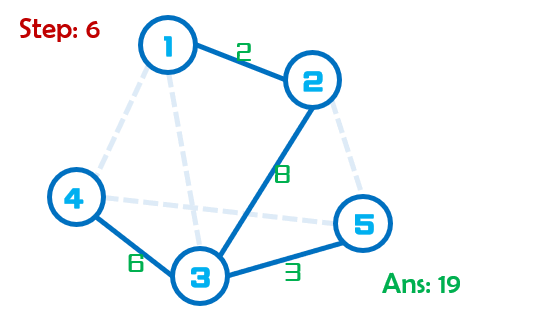
Step：6当前最小边权为8，此时点2,3不在同一集合，因此将点2,3合并到同一个集合。又由于此时(m==n-1)，故算法结束并返回答案：Ans=19。

以上，求图中最小生成树的问题得以解决。

4. 代码实施

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
int n,m,ans,cnt,fa[500100];
struct node{
	int u,v,w;
	bool friend operator <(node a,node b){
		return a.w<b.w;
	}
}edge[500010];
inline int Find(int x){return fa[x]==x? x:fa[x]=Find(fa[x]);}
void Kruskal(){
	sort(edge+1,edge+m+1);//边权排序
	for(int i=1;i<=m;i++){
		int fu=Find(edge[i].u);
		int fv=Find(edge[i].v);
		if(fu==fv) continue;//已经在同一集合，由于再加入这条边会形成环，因此不考虑这条边
		cnt++;//累计生成树中边的条数
		ans+=edge[i].w;//累计答案
		fa[fu]=fv;//合并到同一集合
		if(cnt==n-1) break;//已经得出最小生成树
	}
	if(cnt<n-1){//无法形成生成树
		cnt=0;return;
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++) scanf("%d%d%d",&edge[i].u,&edge[i].v,&edge[i].w);
	for(int i=1;i<=n;i++) fa[i]=i;//并查集初始化
	Kruskal();
	if(cnt) printf("%d",ans);
	else printf("No Answer");
	return 0;
}

---

三、例题

例1：P2212 [USACO14MAR]浇地Watering the Fields

同P1546 最短网络 Agri-Net，P1111 修复公路，P1195 口袋的天空

模板题，具体解释见代码。

Code：

#include<bits/stdc++.h>
#define N 2500
using namespace std;
int n,c,m,px[N],py[N];
int pre[N],ans,cnt;
struct node{
	int u,v,dis;
	bool operator <(const node &other) const{
		return dis<other.dis;
	}
}q[20000000];
inline int find(int x){
	return pre[x]==x ? x:pre[x]=find(pre[x]);
}
inline void Kruskal(){
	for(int i=1;i<=n;i++) pre[i]=i;
	for(int i=1;i<=m;i++){
		int fu=find(q[i].u);
		int fv=find(q[i].v);
		if(fu!=fv){
			pre[fu]=fv;
			ans+=q[i].dis;
			cnt++;
		}
		if(cnt==n-1) break;
	}
	if(cnt==n-1) printf("%d",ans);
	else printf("-1");
}
int main()
{
	scanf("%d%d",&n,&c);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&px[i],&py[i]);
		for(int j=1;j<i;j++){
			int dis=(px[i]-px[j])*(px[i]-px[j])+(py[i]-py[j])*(py[i]-py[j]);//计算费用
			if(dis<c) continue;//费用小于C的水管不会被安装，因此需要不建边
			q[++m].u=i,q[m].v=j,q[m].dis=dis;
		}
	}
	sort(q+1,q+m+1);
	Kruskal();
		return 0;
}

例2：P1550 [USACO08OCT]打井Watering Hole

我们唯一需要解决的问题在于第一口井打在哪里。不妨设一个超级原点，并把每口井与该点相连，边权就是打井的费用。在新图上跑最小生成树，这样就能巧妙地解决问题。

同P1194 买礼物

Code：

#include<bits/stdc++.h>
using namespace std;
int cnt,pre[200000],num,ans,n;
struct node{
	int u,v,w;
	bool operator <(const node &other) const{
		return w<other.w;
	}
}e[200000];
inline void add_edge(int u,int v,int w){
	cnt++;
	e[cnt].u=u;e[cnt].v=v;e[cnt].w=w;
}
inline int Find(int x){
	return x==pre[x]? x:pre[x]=Find(pre[x]);
}
void Kruskal(){
	for(int i=1;i<=cnt;i++){
		int fu=Find(e[i].u);
		int fv=Find(e[i].v);
		if(fu==fv) continue;
		pre[fu]=fv;
		num++;
		ans+=e[i].w;
		if(num==n) break;//由于包含了超级原点的这一条边，因此最后有n条边
	}
}
int main()
{
	int u,v,w;
	scanf("%d",&n);
	for(int i=1;i<=n;i++){//与超级原点建边
		scanf("%d",&w);
		add_edge(0,i,w);
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){
			scanf("%d",&w);
			if(i==j) continue;
			add_edge(i,j,w);
		}
	sort(e+1,e+cnt+1);
	for(int i=0;i<=n;i++) pre[i]=i;
	Kruskal();
	printf("%d",ans);
	return 0;
}

例3：P1547 Out of Hay

求最小生成树中最大的一条边，每次把边加入生成树中不断取最大值即可。

或者，根据其贪心思想，越晚加进来的边权值越大，因此只要让边权不断赋值给答案就能求出最大值。

例4：P1340 兽径管理

每次只增加一条边，因此用Kruskal算法十分方便。

正常排序后标记产生道路的时间，循环m次最小生成树求的答案。

Code：

#include<bits/stdc++.h>
using namespace std;
int pre[1000000],n,m,ans,num;
struct node
{
	int u,v,w,p;
	bool operator <(const node &other)const{
		return w<other.w;
	}
}e[1000000];
inline int Find(int x)
{
	if(pre[x]==x) return x;
	pre[x]=Find(pre[x]);
	return pre[x];
}
void Kruskal(int p)
{
	ans=0;num=0;
	for(int i=1;i<=n;i++) pre[i]=i;
    for(int i=1;i<=m;i++)
    {
    	int fu=Find(e[i].u);
    	int fv=Find(e[i].v);
    	if(fu==fv||e[i].p>p) continue;
    	pre[fu]=fv;
    	ans+=e[i].w;
    	num++;
    	if(num==n-1) {
    		printf("%d\n",ans);break;
		}
	}
	if(num<n-1){
		printf("-1\n");
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		e[i].u=u;e[i].v=v;e[i].w=w;
		e[i].p=i;
	}
	sort(e+1,e+m+1);
	for(int i=1;i<=n;i++) pre[i]=i;
	for(int i=1;i<=m;i++) Kruskal(i);
	return 0;
}

---