poj3784(对顶堆)

题意：多组数据，让你求出1~i(i为奇数&&i<=n)的中位数

思路：首先复杂度必为O(n)或O(nlogn)的（数据范围）

　　　思索，如果题目要求1次中位数，好求！排个序，取a[(n+1)/2]就好了 [这道题n的前提是奇数哈]

　　　可是？？？要求多次中位数，而且是每次加入两个数后，再求一次？

　　　别慌！！！已知中位数的性质是跟数值的顺序有关的。

　　　顺序？大家想一想有哪个数据结构能够动态维护数列顺序，并1次操作复杂度在O(logn)之内

　　　那当然是堆【肯定用优先队列啦】^_^

方式：【对顶堆】

　　　不要太在乎为何叫“对顶堆”，因为我也不知道

　　　通过取中间的数，可以想到维护两个堆:一个大根堆（叫她Qx)，一个小根堆（叫他Qn),这两个堆的大小无论怎样动态变化都恒保持：Qx.size()-Qn.size()=1或0  [Qx.size()总是>=Qn.size()的]

　　　要两个堆的目的大家肯定都能想到了，因为一旦i为奇数要输出时，直接输出Qx.top()就好了。不过这只是脑补出了一些过程，请看下面：

　　　

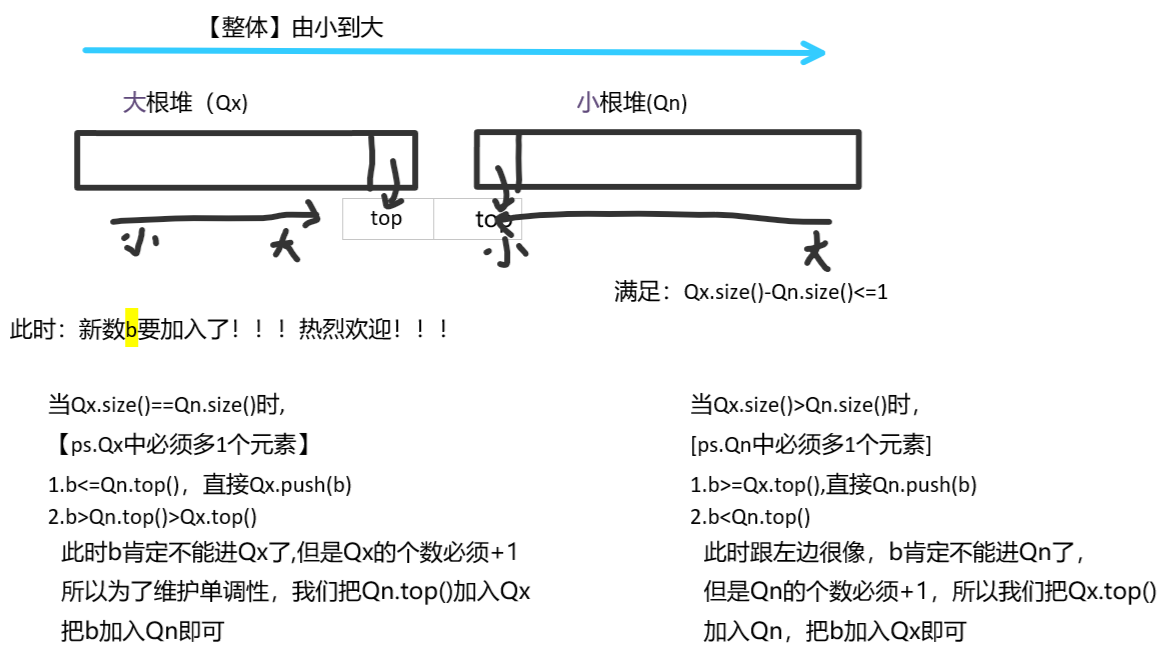
　　　我说的有点啰嗦，大家还是看看代码吧：

#include<stdio.h>
#include<algorithm>
#include<queue>
using namespace std;
priority_queue<int> Qx;
priority_queue<int,vector<int>,greater<int> > Qn;
int main() {
//	freopen("poj3785.out","w",stdout);
	int t;
	scanf("%d",&t);
	while(t--) {
		while(!Qn.empty()) Qn.pop();
		while(!Qx.empty()) Qx.pop();
		int p,n; scanf("%d%d",&p,&n);
		printf("%d %d\n",p,(n+1)/2);
		for(int i=1;i<=n;i++) {
			int b; scanf("%d",&b);
			//之所以要加上特判，因为要保证两个队列都非空，才能不运行错误
			if(i==1) {
				Qx.push(b); printf("%d ",b);
			}
			else if(i==2) {
				if(b<Qx.top()) Qn.push(Qx.top()),Qx.pop(),Qx.push(b);
				else Qn.push(b);
			}
			else if(Qx.size()==Qn.size()) {		//Qx.size()必须+1
				if(b<=Qn.top()) Qx.push(b);
				else {		//b>Qn.top()
					Qx.push(Qn.top()); Qn.pop(); Qn.push(b);	//将小根堆的堆头插入大根堆，并将b插入小根堆
				}
				printf("%d ",Qx.top());
				if(((i+1)/2)%10==0) printf("\n");
			}
			else {	//Qn.size()必须+1
				if(b>=Qx.top()) Qn.push(b);
				else {		//b<Qx.top();
					Qn.push(Qx.top()); Qx.pop(); Qx.push(b);	//有没有觉得是15行的反操作呢？
				}
			}
		}
		if((n+1)/2%10!=0) printf("\n");
	}
	return 0;
}

有什么建议，欢迎讨论