左手坐标系和右手坐标系 ZZ

今天记录一下一些基本的数学知识，左手坐标系和右手坐标系。这些对于搞图像开发或者游戏开发的朋友来说，应该是很基础的东西，不过对于大部分人来说还是比较陌生的知识。之所以看这方面资料主要是因为在使用Android Camera使用Matrix的过程中，发现需要一些数学理论支持才能理解。这是为了后面使用Android Camera和Matrix的基础。

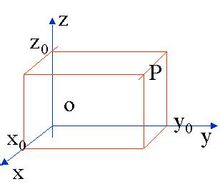
1、空间直角坐标系

　　下面摘录一段百科的解析，这些都是数学基础。过空间定点O作三条互相垂直的数轴,它们都以O为原点,具有相同的单位长度.这三条数轴分别称为X轴(横轴).Y轴(纵轴).Z轴(竖轴),统称为坐标轴。

　　各轴之间的顺序要求符合右手法则,即以右手握住Z轴,让右手的四指从X轴的正向以90度的直角转向Y轴的正向,这时大拇指所指的方向就是Z轴的正向.这样的三个坐标轴构成的坐标系称为右手空间直角坐标系.与之相对应的是左手空间直角坐标系.一般在数学中更常用右手空间直角坐标系，在其他学科方面因应用方便而异。三条坐标轴中的任意两条都可以确定一个平面,称为坐标面.它们是:由X轴及Y轴所确定的XOY平面;由Y轴及Z轴所确定的YOZ平面；由X轴及Z轴所确定的XOZ平面．这三个相互垂直的坐标面把空间分成八个部分，每一部分称为一个卦限．位于X，Y，Z轴的正半轴的卦限称为第一卦限，从第一卦限开始，在XOY平面上方的卦限，按逆时针方向依次称为第二，三，四卦限；第一，二，三，四卦限　下方的卦限依次称为第五，六，七，八卦限。

 

 

 

2、右手坐标系

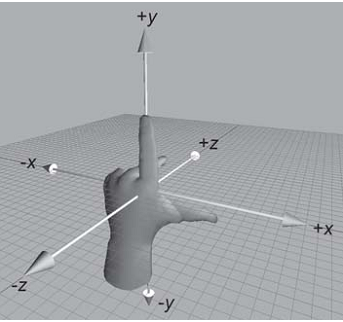
　　右手坐标系在我们以前初中高中学几何的时候也经常用到。在三维坐标系中，Z轴的正轴方向是根据右手定则确定的。右手定则也决定三维空间中任一坐标轴的正旋转方向。要标注X、Y和Z轴的正轴方向，就将右手背对着屏幕放置，拇指即指向X轴的正方向。伸出食指和中指，如右图所示，食指指向Y轴的正方向，中指所指示的方向即是Z轴的正方向。要确定轴的正旋转方向，如下图所示，用右手的大拇指指向轴的正方向，弯曲手指。那么手指所指示的方向即是轴的正旋转方向。

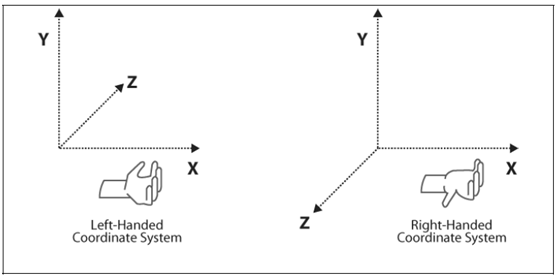
3、左手坐标系

　　伸出左手，让拇指和食指成“L”形，大拇指向右，食指向上。其余的手指指向前方。这样就建立了一个左手坐标系。拇指、食指和其余手指分别代表x，y，z轴的正方向。判断方法：在空间直角坐标系中，让左手拇指指向x轴的正方向，食指指向y轴的正方向，如果中指能指向z轴的正方向，则称这个坐标系为左手直角坐标系．反之则是右手直角坐标系。

 

 

 

4、左手坐标系和右手坐标系比较

　　手坐标系和右手坐标系，左手坐标系是X轴向右，Y轴向上，Z轴向前，右手坐标系的Z轴正好相反，是指向“自己”的，在计算机中通常使用的是左手坐标系，而数学中则通常使用右手坐标系。计算机里面其实很多也有用右手坐标系，这个只是根据实际应用不同，没有说哪个比较好。

 

 

5、结语

　　今天主要是讲讲这两个坐标系和区分，因为后面我会讲解有关Android Camera使用Matrix进行滑动特效变换。里面就好应用到很多坐标系的转换，所以脑袋里面要先有这方面的概念，否则有关Matrix的转换和图像操作就不好理解了。

 

 

Edited by mythou

原创博文，转载请标明出处：http://www.cnblogs.com/mythou/p/3327046.html