POJ 3177 （Redundant Paths） —— （有重边，边双联通，无向图缩点）

　　做到这里以后，总算是觉得tarjan算法已经有点入门了。

　　这题的题意是，给出若干个点和若干条边连接他们，在这个无向图中，问至少增加多少条边可以使得这个图变成边双联通图（即任意两点间都有至少两条没有重复边的路径可以到达，可以经过同一个点。这个条件等价于每一条边都至少在一个环中）。

　　方法：将无向图缩点以后，找出那些度为1的点的个数cnt，那么答案就是(cnt+1)/2。这么一看，好像就是缩点以后使它变成强连通图的意思？大概强连通图是有向图才有的名词吧。。

　　和有向图缩点类似，只要把if(!belong[v])改成if(v != fa)即可，这样，就可以防止同一条边的方向性关系了，而a到b如果是间接到达的话，是没有问题的。还有，通过这题，我明白了为什么tarjan算法里面有一个是用dfn来更新的了。这里来回顾一下：找割点或者桥的时候有low[v]和dfn[u]的比较，如果都是用low更新的话，那么low可能会变小导致漏掉割点或者桥的情况。举割点那篇中的图当例子：http://www.cnblogs.com/zzyDS/p/5629021.html 如这个图，

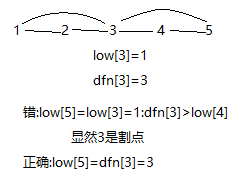
图(v,e)点为1，2，3，4，5，边有(1,2),(2,3),(1,3),(3,4),(4,5),(3,5)，令1为树根。显然3为割点。不妨假设搜索顺序是(1,2),(2,3),(3,1),(3,4),(4,5),(5,3)，搜索到(3,1)的时候，更新low[3] = dfn[1] = 1，然后搜索(3,4)、(4,5)，(5,3)，发现3已经遍历，那么如果此时采用low[u] = min(low[u], low[v])的话，会更新low[5] = low[3] = 1，回溯到4，low[4] = low[5] = 1，回溯到3，low[3] = low[4] = 1，然后比较发现low[4] < dfn[3]，判断出3不是割点，算法错误。反正以后都用dfn更新应该就对了- -还有一点想说的是，用dfn的好处在于，不需要belong数组了，只要low一样的那么他们缩点以后都属于一个点（这个说法是错误的！上面这个图就是反例，上面那个图缩点以后还是只有一个点了，所以还是老老实实的用belong数组吧）。

　　另外，这题比较有意思的地方在于，题目给定，两个点之间如果有重边，只算一条。那么就引发了一大堆有意思的讨论了。

　　先给出最初的代码（WA的，因为没判断重边）：

 #include <stdio.h>
 #include <stack>
 #include <algorithm>
 #include <string.h>
 #include <vector>
 using namespace std;

 const int N = +;

 stack<int> S;
 int dfs_clock;
 int dfn[N];
 int low[N];
 vector<int> G[N];
 int n,r;
 int du[N];

 void dfs(int u,int fa)
 {
     dfn[u] = low[u] = ++dfs_clock;
     for(int i=;i<G[u].size();i++)
     {
         int v = G[u][i];
         if(!dfn[v])
         {
             dfs(v,u);
             low[u] = min(low[u],low[v]);
         }
         else if(v != fa)
         {
             low[u] = min(low[u],dfn[v]);
         }
     }
 }

 void solve()
 {
     for(int i=;i<=n;i++)
     {
         if(!dfn[i]) dfs(i,-);
     }

     for(int i=;i<=n;i++)
     {
         for(int j=;j<G[i].size();j++)
         {
             int v = G[i][j];
             if(low[i]!=low[v]) du[low[i]]++;
         }
     }

     int cnt=;
     for(int i=;i<=dfs_clock;i++) if(du[i]==) cnt++;
     printf("%d\n",(cnt+)/);
 }

 void init()
 {
     for(int i=;i<=n;i++) G[i].clear();
     dfs_clock=;
     memset(dfn,,sizeof(dfn));
     memset(du,,sizeof(du));
 }

 int main()
 {
     while(scanf("%d%d",&n,&r)==)
     {
         init();

         for(int i=;i<=r;i++)
         {
             int u,v;
             scanf("%d%d",&u,&v);
             G[u].push_back(v);
             G[v].push_back(u);
         }
         solve();
     }
     return ;
 }

　　然后由于这题给的边是5000，可以用邻接矩阵来做，但是要注意用bool数组，不然超内存。代码如下：

 #include <stdio.h>
 #include <stack>
 #include <algorithm>
 #include <string.h>
 #include <vector>
 using namespace std;

 const int N = +;

 int dfs_clock;
 int dfn[N];
 int low[N];
 int n,r;
 int du[N];
 bool mp[N][N];

 void dfs(int u,int fa)
 {
     dfn[u] = low[u] = ++dfs_clock;
     for(int i=;i<=n;i++)
     {
         if(!mp[u][i]) continue;
         if(!dfn[i])
         {
             dfs(i,u);
             low[u] = min(low[u],low[i]);
         }
         else if(i != fa)
         {
             low[u] = min(low[u],dfn[i]);
         }
     }
 }

 void solve()
 {
     for(int i=;i<=n;i++)
     {
         if(!dfn[i]) dfs(i,-);
     }

     for(int i=;i<=n;i++)
     {
         for(int j=;j<=n;j++)
         {
             if(!mp[i][j]) continue;
             if(low[i]!=low[j]) du[low[i]]++;
         }
     }

     int cnt=;
     for(int i=;i<=dfs_clock;i++) if(du[i]==) cnt++;
     printf("%d\n",(cnt+)/);
 }

 void init()
 {
     memset(mp,,sizeof(mp));
     dfs_clock=;
     memset(dfn,,sizeof(dfn));
     memset(du,,sizeof(du));
 }

 int main()
 {
     while(scanf("%d%d",&n,&r)==)
     {
         init();

         for(int i=;i<=r;i++)
         {
             int u,v;
             scanf("%d%d",&u,&v);
             if(mp[u][v]) continue;
             mp[u][v]=mp[v][u]=;
         }
         solve();
     }
     return ;
 }

　　然后要判重的话，可以用大力学长的set法，把边用pair记录然后全部丢进set里面用find来查找即可，代码如下：

 #include<iostream>
 #include<cstdio>
 #include<string>
 #include<cstring>
 #include<map>
 #include<queue>
 #include<stack>
 #include<algorithm>
 #include<cmath>
 #include<set>
 #include<vector>
 using namespace std;
 typedef long long ll;
 typedef long long LL;
 #define MP make_pair
 #define PII pair<int,int>
 #define PFI pair<double,int>
 #define F first
 #define S second
 #define lson l,mid,rt<<1
 #define rson mid+1,r,rt<<1|1
 const int INF = 0x7f7f7f7f;
 const int MOD = ;
 const double eps = 1e-;
 const int maxn =  + ;

 const int N =  + ;
 int n,m;
 vector<vector<int> > G(N);
 int scc_cnt,dfs_clock,belong[N],dfn[N],low[N];
 bool instack[N];
 stack<int> S;
 set<pair<int,int> > st;
 void dfs(int u,int fa){
     low[u] = dfn[u] = ++ dfs_clock;
     S.push(u);
     for(int i =  ; i < G[u].size() ; i ++){
         int v = G[u][i];
         if(v == fa) continue; // 无向图 a-b: 防止b访问a(父亲)
         if(!dfn[v]){
             dfs(v,u);
             low[u] = min(low[u],low[v]);
         }else if(!belong[v]){
             low[u] = min(low[u],dfn[v]);
         }
     }
     if(low[u] == dfn[u]){
         scc_cnt ++;
         for(;;){
             int x = S.top(); S.pop();
             belong[x] = scc_cnt; // 缩点。
             if(x == u) break;
         }
     }
 }
 void scc(){
     scc_cnt = dfs_clock = ;
     memset(belong,,sizeof(belong));
     memset(dfn,,sizeof(dfn));
     memset(low,,sizeof(low));
     memset(instack,false,sizeof(instack));
     while(!S.empty()) S.pop();
     for(int i =  ; i <= n ; i ++){
         if(!dfn[i]) dfs(i,-);
     }
     int deg[N];
     memset(deg,,sizeof(deg));
     for(int i =  ; i <= n ; i ++){
         for(int j =  ; j < G[i].size() ; j ++){
             int v = G[i][j];
             if(belong[i] != belong[v]){
                 deg[ belong[i] ] ++;
                 deg[ belong[v] ] ++;
             }
         }
     }
     int cnt = ;
     for(int i =  ; i <= n ; i++){
         if(deg[i] /  == ) cnt ++;
     }
     cout << (cnt + ) /  << endl;
 }
 int main(){
     while(scanf("%d%d",&n,&m) != EOF){
         for(int i =  ; i <= n ; i ++) G[i].clear();
         st.clear();
         for(int i =  ; i < m ; i ++){
             int u,v;
             scanf("%d%d",&u,&v);
             // 判重边。
             if(st.find(MP(u,v)) != st.end()) continue;
             if(st.find(MP(v,u)) != st.end()) continue;
             st.insert(MP(u,v));
             st.insert(MP(v,u));
             G[u].push_back(v);
             G[v].push_back(u);
         }
         scc();
     }
     return ;
 }

　　最后，我想，既然要判重，干脆不用vector了，直接用set吧- -！代码如下：

 #include <stdio.h>
 #include <stack>
 #include <algorithm>
 #include <string.h>
 #include <vector>
 #include <set>
 using namespace std;

 const int N = +;

 stack<int> S;
 int dfs_clock;
 int dfn[N];
 int low[N];
 set<int> G[N];
 int n,r;
 int du[N];

 void dfs(int u,int fa)
 {
     dfn[u] = low[u] = ++dfs_clock;
     for(set<int>::iterator it=G[u].begin();it!=G[u].end();it++)
     {
         int v = *it;
         if(!dfn[v])
         {
             dfs(v,u);
             low[u] = min(low[u],low[v]);
         }
         else if(v != fa)
         {
             low[u] = min(low[u],dfn[v]);
         }
     }
 }

 void solve()
 {
     for(int i=;i<=n;i++)
     {
         if(!dfn[i]) dfs(i,-);
     }

     for(int i=;i<=n;i++)
     {
         for(set<int>::iterator it=G[i].begin();it!=G[i].end();it++)
         {
             int v = *it;
             if(low[i]!=low[v]) du[low[i]]++;
         }
     }

     int cnt=;
     for(int i=;i<=dfs_clock;i++) if(du[i]==) cnt++;
     printf("%d\n",(cnt+)/);
 }

 void init()
 {
     for(int i=;i<=n;i++) G[i].clear();
     dfs_clock=;
     memset(dfn,,sizeof(dfn));
     memset(du,,sizeof(du));
 }

 int main()
 {
     while(scanf("%d%d",&n,&r)==)
     {
         init();

         for(int i=;i<=r;i++)
         {
             int u,v;
             scanf("%d%d",&u,&v);
             G[u].insert(v);
             G[v].insert(u);
         }
         solve();
     }
     return ;
 }