Minimum Score Triangulation of Polygon

Given N, consider a convex N-sided polygon with vertices labelled A[0], A[i], ..., A[N-1] in clockwise order.

Suppose you triangulate the polygon into N-2 triangles.  For each triangle, the value of that triangle is the product of the labels of the vertices, and the total score of the triangulation is the sum of these values over all N-2triangles in the triangulation.

Return the smallest possible total score that you can achieve with some triangulation of the polygon.

Example 1:

Input: [1,2,3]
Output: 6
Explanation: The polygon is already triangulated, and the score of the only triangle is 6.

Example 2:

Input: [3,7,4,5]
Output: 144
Explanation: There are two triangulations, with possible scores: 3*7*5 + 4*5*7 = 245, or 3*4*5 + 3*4*7 = 144.  The minimum score is 144.

Example 3:

Input: [1,3,1,4,1,5]
Output: 13
Explanation: The minimum score triangulation has score 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13.

分析：https://leetcode.com/problems/minimum-score-triangulation-of-polygon/discuss/286753/C%2B%2B-with-picture

If we pick a side of our polygon, it can form n - 2 triangles. Each such triangle forms 2 sub-polygons. We can analyze n - 2 triangles, and get the minimum score for sub-polygons using the recursion.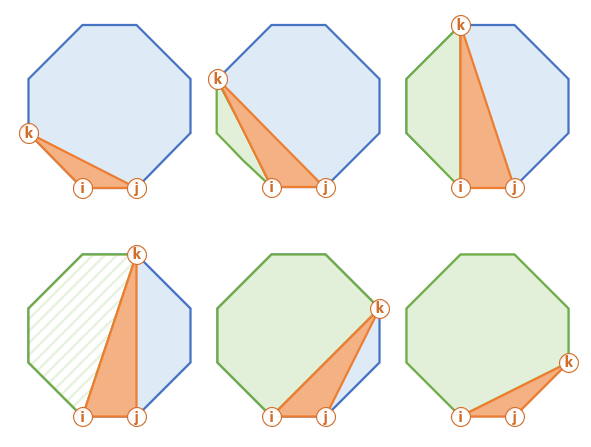

This is how this procedure looks for a sub-polygon (filled with diagonal pattern above).

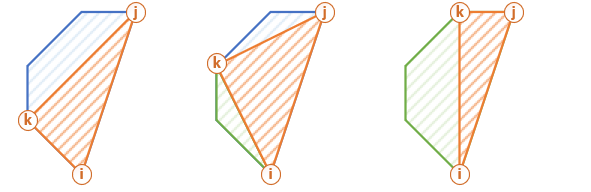
Top-Down Solution

• Fix one side of the polygon i, j and move k within (i, j).
• Calculate score of the i, k, j "orange" triangle.
• Add the score of the "green" polygon i, k using recursion.
• Add the score of the "blue" polygon k, j using recursion.
• Use memoisation to remember minimum scores for each sub-polygons.

class Solution {
    public int minScoreTriangulation(int[] arr) {
        int len = arr.length;
        int[][] lookup = new int[len][len];
        return minScoreFromTo(arr, , len - , lookup);
    }

    private int minScoreFromTo(int[] arr, int from, int to, int[][] lookup) {
        if (from >= to || from +  == to) {
            return ;
        }
        if (lookup[from][to] > ) {
            return lookup[from][to];
        }
        lookup[from][to] = Integer.MAX_VALUE;
        for (int mid = from + ; mid < to; mid++) {
            lookup[from][to] = Math.min(lookup[from][to], arr[mid] * arr[from] * arr[to] + minScoreFromTo(arr, from, mid, lookup)
                    + minScoreFromTo(arr, mid, to, lookup));
        }
        return lookup[from][to];
    }
}