建模算法（八）——插值

插值：求过已知有限个数据点的近似函数

拟合：已知有限个数据点，求近似函数，不要求过已知数据点，只要求在某种意义下在这些点的误差最小

（一）插值方法

一、拉格朗日多项式插值

1、插值多项式

就是做出一个多项式函数，经过给出的n个节点，并尽可能的接近原函数，将点带入多项式函数得到一个线性方程组

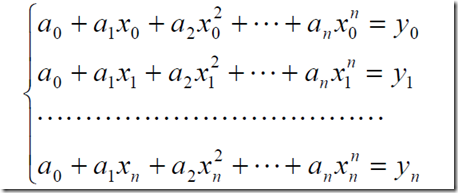
当系数矩阵满秩时，有唯一解。而，系数矩阵的行列式为

这是一个范德蒙德行列式，只要各个节点不同时，行列式就不为0，因此可得，一定能够解出系数方程

还有些指标

2、拉格朗日插值多项式

3、MATLAB实现

function y=lagrange(x0,y0,x)

%n个数据以数组x0,y0输入，m个插值点以数组x输入，输出数组y为m个插值。
n=length(x0);m=length(x);
for i=m;
    z=x(i);
    s=0.0;
    for k=1:n
        p=1.0;
        for j=1:n;
            if j~=k
            p=p*(z-x0(j))/(x0(k)-x0(j));
            end
        end
        s=p*y0(k)+s;
    end
    y(i)=s;
end

二、牛顿插值

1、差商

2、牛顿插值公式

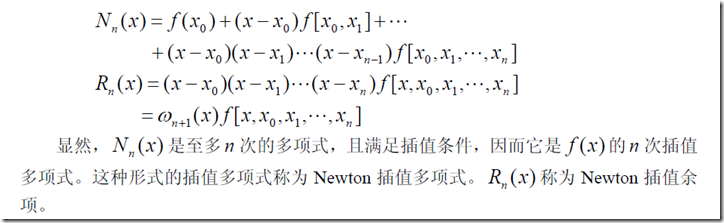
有点就是，多一个数据点，只多一项

PS：

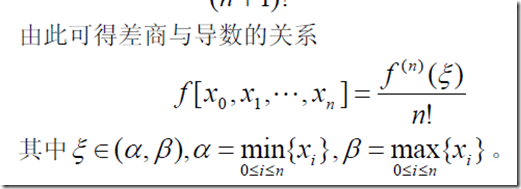
3、差分

4、等距节点插值公式

三、分段线性插值

1、插值多项式的振荡

即如果插值多项式的次数越高，越容易发生振荡，不能很好的拟合。

2、分段线性插值

3、MATLAB实现

四、Hermite插值

1、Hermite插值多项式

2、MATLAB实现

function y-hermite(x0,y0,y1,x);
%x0,y0为样本点数据，y1为导数指，m个插值点以数组x输入，输出数组y为m个插值
n=length(x0);m=length(x);
for k=1:m;
    yy=0.0;
    for i=1:n
        h=1.0;
        a=0.0;
        for j=i:n
            if j~=i
                h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2;
                a=1/(x0(i)-x0(j))+a;
            end
        end
        yy=yy+h*((x0(i)-x0(k))*(2*a*y0(i)-y(i))+y0(i));
    end
    y(k)=yy;
end

五、样条插值

1、概念

实际中最常用的是k=2和k=3的情况

二、二次样条函数插值

二次样条函数有n+2个待定常数，所以要有n+2个条件，才能有唯一解

一定要有一个条件为一阶导数

三、三次样本函数插值

二次样条函数有n+3个待定常数，所以要有n+3个条件，才能有唯一解

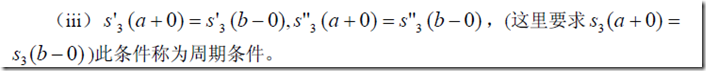
四、三次插值在MATLAB中的实现

部分转载

1、y=interp1(x0,y0,x,`spline`);     % (spline改成linear，则变成线性插值)

2、y=spline(x0,y0,xi);%这个是根据己知的x，y数据，用样条函数插值出xi处的值。即由x,y的值计算出xi对应的函数值。

3、pp=spline(x0,y0);%是由根据己知的x，y数据，求出它的样条函数表达式，不过该表达式不是用矩阵直接表示，要求点x`的值，要用函数y`=ppval(pp,x`);

4、pp=csape(x,y,'变界类型','边界值conds');生成各种边界条件的三次样条插值. 其中,(x,y)为数据向量,边界类型可为:

'complete'：给定边界一阶导数,即默认的边界条件,Lagrange边界条件
             'not-a-knot'：非扭结条件,不用给边界值.
             'periodic'：周期性边界条件,不用给边界值.
             'second'：给定边界二阶导数.
             'variational'：自然样条(边界二阶导数为[0,0]。

五、demo

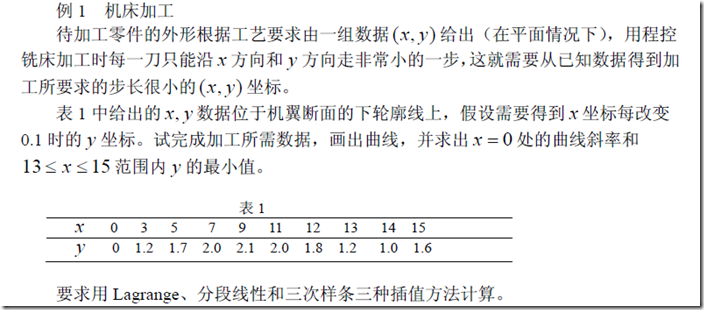
%转载= =

clear,clc
x0=[0,3,5,7,9,11,12,13,14,15];
y0=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6];
t=0:0.05:15;
%拉格朗日插值函数
y1=lagrange(x0,y0,t);%调用编写的lagrange函数
dy1=(lagrange(x0,y0,0.0001)-lagrange(x0,y0,0))/0.0001%x=0处斜率
min1=min(lagrange(x0,y0,13:0.001:15))%13到15最小值
subplot(2,2,1);
plot(x0,y0,'ro',t,y1);%画出曲线
title('拉格朗日插值函数');
%分段线性插值
y2=interp1(x0,y0,t,'spline');%注意区分spline与linear
Y2=interp1(x0,y0,t);%默认linear
dy2=(interp1(x0,y0,0.0001,'spline')-interp1(x0,y0,0,'spline'))/0.0001%x=0处斜率
min2=min(interp1(x0,y0,13:0.001:15,'spline'))%13到15最小值
subplot(2,2,2);
plot(t,y2,'b',t,Y2,'r',x0,y0,'ro');%画出曲线
title('分段线性插值');
legend('边条','线性');%显示图形图例
%三次线条插值A
y3=spline(x0,y0,t);
dy3=(spline(x0,y0,0.0001)-spline(x0,y0,0))/0.0001%x=0处斜率
min3=min(spline(x0,y0,13:0.001:15))%13到15最小值
subplot(2,2,3);
plot(x0,y0,'ro',t,y3);%画出曲线
title('三次线条插值A');
%三次线条插值B
pp1=csape(x0,y0);%默认的边界条件,即给定边界一阶导数
pp2=csape(x0,y0,'second');%给定边界二阶导数
y4=ppval(pp1,t);
Y4=ppval(pp2,t);
dy4=(ppval(pp1,0.0001)-ppval(pp1,0))/0.0001%x=0处斜率
min4=min(ppval(pp1,13:0.001:15))%13到15最小值
subplot(2,2,4);
plot(t,y4,'b',t,Y4,'r',x0,y0,'ro');%画出曲线
title('三次线条插值B');
legend('一阶','二阶');

七、二维插值

如果节点是二维的，插值函数是二元函数的话（曲面），我们可以画出三维的效果图

1、插值节点为网络节点

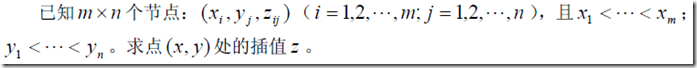
MatLab封装程序

z=interp2(x0,y0,z0,x,y,'method')

a、x0,y0为节点坐标，z0为n*m维矩阵，表示节点的值

b、x0,y0要求一个为行向量一个为列向量

c、z为矩阵，n=length(y)，m=length(x)       因为MATLAB是列优先

d、

e、x,y为插值点坐标，z为函数值

然后如果是三次样条插值，可以使用命令

pp=csape({x0,y0},z0,conds,valconds),z=fnval(pp,{x,y})

a、x0,y0为节点坐标，z0为n*m维矩阵，表示节点的值

b、x0,y0要求一个为行向量一个为列向量

c、“conds”与一维相同，一般默认

d、x,y为插值点坐标 ，z为函数值

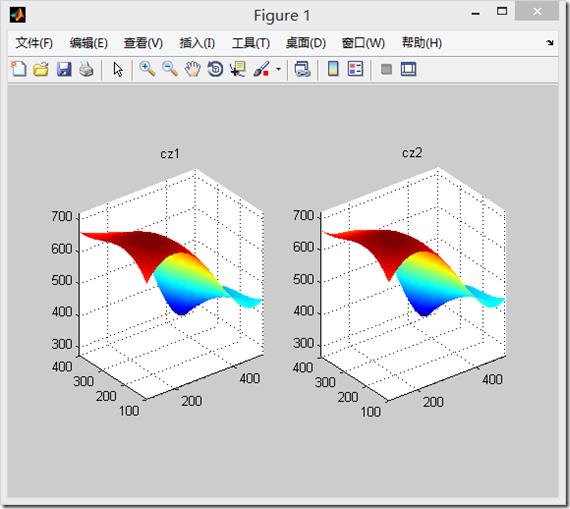
2、demo

clear,clc

%样本点信息
x=100:100:500;
y=100:100:400;

z=[636   697   624  478   450
   698   712   630  478   420
   680   674   598  412   400
   662   626   552  334   310];

%录入样本点信息
pp=csape({x,y},z');  %注意z矩阵的行列所对应的向量
xi=100:10:500;
yi=100:10:400;
cz1=fnval(pp,{xi,yi});

cz2=interp2(x,y,z,xi,yi','spline');
[i,j]=find(cz1==max(max(cz1)))

subplot(1,2,1);
surf(xi,yi,cz1');
shading interp;   %插入颜色插值
axis equal;
title('cz1');

subplot(1,2,2);
surf(xi,yi,cz2);
shading interp;
axis equal;
title('cz2');

二、插值节点为散乱节点

1、定义

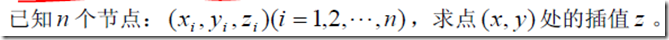
MATLAB提供了一个函数

zi=griddata(x,y,z,xi,yi)

a、x,y,z为n维向量，就是数据点

b、xi,yi是给定的网格点横纵坐标（插值点），返回zi的值

2、demo

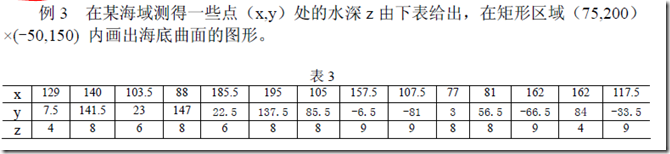
clear,clc

%样本点信息
x=[129,140,103.5,88,185.5  195  105  157.5  107.5   77   81  162   162   117.5];
y=[7.5   141.5  23  147   22.5   137.5  85.5   -6.5   -81   3  56.5   -66.5  84  -33.5];
z=-[4   8  6 8  6  8  8  9  9  8  8  9  4  9];

xi=75:200;
yi=-50:150;
zi=griddata(x,y,z,xi,yi','cubic');

subplot(1,2,1);
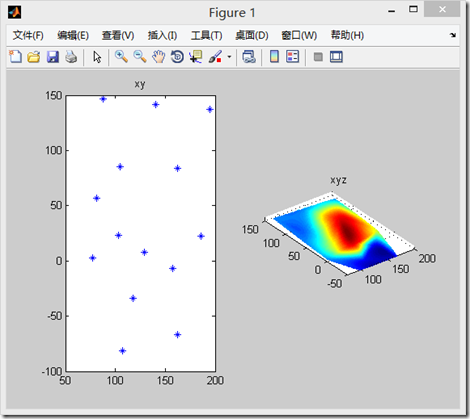
plot(x,y,'*');
title('xy');

subplot(1,2,2);
mesh(xi,yi,zi);
shading interp;
axis equal;
title('xyz');