POJ2676Sudoku(类似于八皇后)
| Time Limit: 2000MS | Memory Limit: 65536K | |||
| Total Submissions: 16444 | Accepted: 8035 | Special Judge | ||
Description
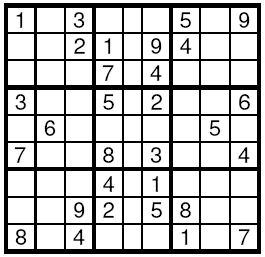
Input
Output
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
Source
题意:每行每列每个小的九宫格 每个数字只出现一次;
看着很高大上的题目做起来这么好玩,搜索真是很神奇!应该是第一次写带有返回值的搜索
转载请注明出处:優YoU http://user.qzone.qq.com/289065406/blog/1303713313
大致题意:
九宫格问题,也有人叫数独问题
把一个9行9列的网格,再细分为9个3*3的子网格,要求每行、每列、每个子网格内都只能使用一次1~9中的一个数字,即每行、每列、每个子网格内都不允许出现相同的数字。
0是待填位置,其他均为已填入的数字。
要求填完九宫格并输出(如果有多种结果,则只需输出其中一种)
如果给定的九宫格无法按要求填出来,则输出原来所输入的未填的九宫格
解题思路:
DFS试探,失败则回溯
用三个数组进行标记每行、每列、每个子网格已用的数字,用于剪枝
bool row[10][10]; //row[i][x] 标记在第i行中数字x是否出现了
bool col[10][10]; //col[j][y] 标记在第j列中数字y是否出现了
bool grid[10][10]; //grid[k][x] 标记在第k个3*3子格中数字z是否出现了
row 和 col的标记比较好处理,关键是找出grid子网格的序号与 行i列j的关系
即要知道第i行j列的数字是属于哪个子网格的
首先我们假设子网格的序号如下编排:
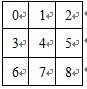
由于1<=i、j<=9,我们有: (其中“/”是C++中对整数的除法)
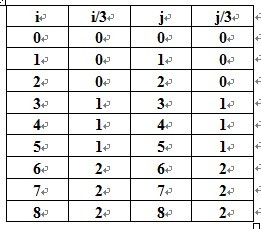
令a= i/3 , b= j/3 ,根据九宫格的 行列 与 子网格 的 关系,我们有:
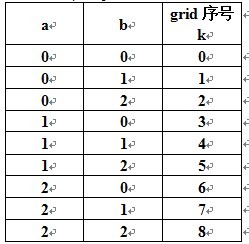
不难发现 3a+b=k
即 3*(i/3)+j/3=k
又我在程序中使用的数组下标为 1~9,grid编号也为1~9
因此上面的关系式可变形为 3*((i-1)/3)+(j-1)/3+1=k
有了这个推导的关系式,问题的处理就变得非常简单了,直接DFS即可
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio> using namespace std;
int row[][],col[][],grid[][];
int g[][];
bool dfs(int x,int y)
{
if(x == )
{
return true;
}
bool flag = false;
if(g[x][y])
{
if(y == )
{
flag = dfs(x + , );
}
else
{
flag = dfs(x, y + );
}
if(flag)
return true;
else
return false;
}
else if(g[x][y] == )
{
for(int i = ; i <= ; i++)
{
int k = (x - ) / * + (y - ) / + ;
if(col[y][i] == && row[x][i] == && grid[k][i] == )
{
g[x][y] = i;
col[y][i] = ;
row[x][i] = ;
grid[k][i] = ;
if(y < )
{
flag = dfs(x,y + );
}
else
{
flag = dfs(x + , );
}
if(flag == false)
{
g[x][y] = ;
col[y][i] = ;
row[x][i] = ;
grid[k][i] = ;
}
else
return true;
}
}
}
return false;
}
int main()
{
int t;
scanf("%d", &t);
getchar();
while(t--)
{
memset(row,,sizeof(row));
memset(col,,sizeof(col));
memset(grid,,sizeof(grid));
memset(g,,sizeof(g));
char ch;
for(int i = ; i <= ; i++)
{
for(int j = ; j <= ; j++)
{
scanf("%c", &ch);
if(ch != '')
{
g[i][j] = ch - '';
row[i][ch - ''] = ;
col[j][ch - ''] = ;
int k = (i - ) / * + (j - ) / + ;
grid[k][ch - ''] = ;
}
}
getchar();
}
dfs(,);
for(int i = ; i <= ; i ++)
{
for(int j = ; j <= ; j++)
{
printf("%d",g[i][j]);
}
printf("\n");
}
}
return ;
}
POJ2676Sudoku(类似于八皇后)的更多相关文章
- POJ 1321 棋盘问题【DFS/回溯/放与不放/类似n皇后】
棋盘问题 Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 62164 Accepted: 29754 Description 在一 ...
- 回溯算法——解决n皇后问题
所谓回溯(backtracking)是通过系统地搜索求解问题的方法.这种方法适用于类似于八皇后这样的问题:求得问题的一个解比较困难,但是检查一个棋局是否构成解很容易. 不多说,放上n皇后的回溯问题代码 ...
- 2n皇后问题-------递归 暴力求解题与分布讨论题
问题描述 给定一个n*n的棋盘,棋盘中有一些位置不能放皇后.现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行.同一列或同一条对角线上,任意的两个白皇后都不在同一行.同一列或同一 ...
- 二模12day1解题报告
T1.笨笨与电影票(ticket) 有n个1和m个0,求每个数前1的个数都大于等于0的个数的排列数. 非常坑的一道题,推导过程很烦.首先求出所有排列数是 C(n+m,m),然后算不合法的个数. 假设存 ...
- Codevs p1004 四子连棋
四子连棋 题目描述 Description 在一个4*4的棋盘上摆放了14颗棋子,其中有7颗白色棋子,7颗黑色棋子,有两个空白地带,任何一颗黑白棋子都可以向 ...
- leetcode 39 Combination Sum --- java
Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C wher ...
- HDU 1045(炮台安置 DFS)
题意是在 n*n 的方格中进行炮台的安置,炮台不能处于同一行或同一列(类似于八皇后问题),但若是炮台间有墙壁阻挡,则可以同时安置这对炮台.问图中可以安放的最大炮台数目. 用深搜的方法,若此处为空地,则 ...
- POJ1321 棋盘问题 —— DFS回溯
题目链接:http://poj.org/problem?id=1321 棋盘问题 Time Limit: 1000MS Memory Limit: 10000K Total Submissions ...
- USACO1.5 Checker Challenge(类n皇后问题)
B - B Time Limit:1000MS Memory Limit:16000KB 64bit IO Format:%lld & %llu Description E ...
随机推荐
- 一个简单的python爬虫,以豆瓣妹子“http://www.dbmeizi.com/category/2?p= ”为例
本想抓取网易摄影上的图,但发现查看html源代码时找不到图片的url,但firebug却能定位得到.(不知道为什么???) 目标是抓取前50页的爆乳图,代码如下: import urllib2,url ...
- f2fs解析(六)
f2fs中有对一个bitmap进行操作的函数,感觉很巧妙,和大家分享一下: 1333 static inline void f2fs_change_bit(unsigned int nr, char ...
- 20Spring_JdbcTemplatem模板工具类
JdbcTemplate 是Spring提供简化Jdbc开发模板工具类.为了更好的了解整个JdbcTemplate配置数据库连接池的过程,这篇文章不采用配置文件的方式,而是采用最基本的代码 的方式来写 ...
- ubuntu中启用ssh服务
ssh程序分为有客户端程序openssh-client和服务端程序openssh-server.如果需要ssh登陆到别的电脑,需要安装openssh-client,该程序ubuntu是默认安装的.而如 ...
- Java连接Elasticsearch集群
package cn.test; import java.net.InetAddress; import java.net.UnknownHostException; import org.elast ...
- solaris之复习
1.在vmware 下面加一个硬盘 参考资料:http://bbs.51cto.com/thread-483151-1.html VMWare上solaris 加硬盘的方法(笨办法及新思路 ...
- PHP基础01:环境搭建
1.只会前端的只是有时候让我感到很苦恼,所以决定从今天开始学习后端,看了一些关于后端语言的比较帖子,决定选择php作为我的第一门后端语言.这个是我自己的学习笔记.方便自己复习,不写下来会太无聊了. 第 ...
- REST签名认证
139 开放平台与应用之间以REST协议进行通讯,为了保证通信的安全性,开放平台加入签名认证机制.应用一旦创建,系统生成唯一并且不公开的secretkey,只有应用的拥有者和开放平台知道.因此,当应用 ...
- livewriter写Blog 神秘失踪?
现在习惯用livewriter来总结/记录一些知识并发布为Blog 与同行交流,但是今天发生了一个怪事,上午我整理了两篇文档当时就用livewriter发送到了Blog上,但是晚上来看的时候之前发送的 ...
- Ubuntu Navicat for MySQL安装以及破解方案
今天发现Navicat for MySQL有LINUX版本了哈, 开心的说,首先上官网上下载LINUX版本: http://www.navicat.com/download 1. 下载 navicat ...
