PBR Step by Step（一）立体角

转载请注明出处:http://www.cnblogs.com/jerrycg/p/4924761.html 

本系列从零起步，作为学习笔记与大家分享，从基础的数学和图形理论，一步一步实现基于物理的渲染。

Reference：《PBRT》、《Ray Tracing from the Ground Up》

由于光源是三维空间中的辐射光能，对于其传播范围通常使用立体角来描述，先来看一下什么是立体角。

立体角Solid Angles

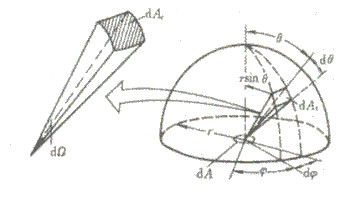
立体角表示一个锥面所围成的空间部分，用符号\(\omega \)表示。

立体角是以圆锥体的顶点为心，半径为r的球面被锥面所截得的面积来度量的，度量单位为“球面度”（steradian，符号∶sr）。球面度表示为三维弧度。

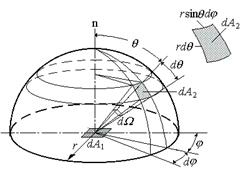
在球坐标系中，球面的极小面积\({dA}_{2}\)为：

\({dA}_{2}=({r}\,\sin\theta\, {d}\varphi )({r\,d\theta })={r}^{2}(\sin\theta\,{d\theta }\,{d}\varphi)\)

整个球面面积为\({dA}\)的积分：

\({A}=\int {dA}_{2}=\int_{0}^{2\pi}\int_{0}^{\pi}({r}\,\sin\theta\, {d}\varphi*{r\,d\theta })={r}^{2}\int_{0}^{2\pi}{d}\varphi\int_{0}^{\pi}\sin\theta\,{d}\theta\)

极小立体角定义为球面面积与球半径平方的比值，即：

\({d\omega} = \frac{dA}{{r}^{2}}=\sin\theta\,{d}\theta\,{d}\varphi\)

对上式积分：

\({\omega} = \int_{0}^{2\pi }{d\varphi }\int_{0}^{\pi } \sin \theta\, {d\theta }={4\pi }\)

可知，最大立体角就是单位球体的表面积。

半球积分

半球积分方程表示为：\({I} = \int_{\omega}{f(\theta, \phi)\cos \theta \, d\omega}\)

其中，\({(\theta, \phi)} \in {[0, \frac{\pi}{2}] [0, 2\pi]}\)，\({\omega \in [0, 2\pi]}\)，\(\cos\theta \, d\omega\)表示立体角在水平面\({(x, y)}\)上的投影，又称为投影立体角。

当函数\({f(\theta, \phi)} = \cos^{n-1} \theta \)时，

\({I} = \int_{2\pi} \cos^{n} \theta \, {d\omega}\)

\(= \int_{0}^{2\pi} \int_{0}^{\frac{\pi}{2}}{\cos^{n}\theta \sin\theta \, d\phi}\)

\(= \int_{0}^{2\pi} d\phi \int_{0}^{2\pi} {\cos^{n}\theta \sin\theta \, d\theta} \)

\(= {2\pi \int_{0}^{\frac{\pi}{2}} \cos^{n}\theta \, \sin\theta \, d\theta}\)

\(= {2\pi \left[\frac{{\cos\theta}^{n+1}}{n+1} \right]_{0}^{\frac{\pi}{2}}} = \frac{2\pi}{n+1}\)

最终得出当\({f(\theta, \phi)} = \cos^{n-1} \theta \)时，半球积分为：\({I} = \frac{2\pi}{n+1}\)