HDOJ 5017 Ellipsoid

第一次尝试模拟退火.....

Ellipsoid

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Total Submission(s): 916    Accepted Submission(s): 305

Special Judge

Problem Description

Given a 3-dimension ellipsoid(椭球面)




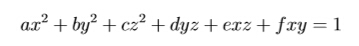
your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x₁,y₁,z₁) and (x₂,y₂,z₂) is defined as 

 

Input

There are multiple test cases. Please process till EOF.



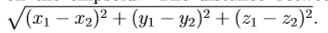
For each testcase, one line contains 6 real number a,b,c(0 < a,b,c,< 1),d,e,f(0 ≤ d,e,f < 1), as described above. It is guaranteed that the input data forms a ellipsoid.All numbers are fit in double.

 

Output

For each test contains one line. Describes the minimal distance. Answer will be considered as correct if their absolute error is less than 10^-5.

 

Sample Input

1 0.04 0.01 0 0 0

 

Sample Output

1.0000000

 

Source

2014 ACM/ICPC Asia Regional Xi'an Online

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const double eps=1e-8;
const double r=0.99;
const int dir_x[8]={0,0,1,-1,1,-1,1,-1};
const int dir_y[8]={1,-1,0,0,-1,1,1,-1};

double a,b,c,d,e,f;

double DIST(double x,double y,double z)
{
	return sqrt(x*x+y*y+z*z);
}

double getZ(double x,double y)
{
	double A=c,B=e*x+d*y,C=a*x*x+b*y*y+f*x*y-1;
	double delta=B*B-4*A*C;
	if(delta<0) return 1e60;
	double z1=(-B+sqrt(delta))/2/A;
	double z2=(-B-sqrt(delta))/2/A;
	if(z1*z1<z2*z2) return z1;
	return z2;
}

double solve()
{
	double step=1;
	double x=0,y=0,z;
	while(step>eps)
	{
		z=getZ(x,y);
		for(int i=0;i<8;i++)
		{
			double nx=x+dir_x[i]*step;
			double ny=y+dir_y[i]*step;
			double nz=getZ(nx,ny);
			if(nz>1e30) continue;
			if(DIST(nx,ny,nz)<DIST(x,y,z))
			{
				x=nx;y=ny;z=nz;
			}
		}
		step=step*r;
	}
	return DIST(x,y,z);
}

int main()
{
	while(scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f)!=EOF)
	{
		printf("%.8lf\n",solve());
	}
	return 0;
}