(简单) POJ 3087 Shuffle'm Up，枚举。

　　Description

　　A common pastime for poker players at a poker table is to shuffle stacks of chips. Shuffling chips is performed by starting with two stacks of poker chips, S₁ and S₂, each stack containing C chips. Each stack may contain chips of several different colors.

　　The actual shuffle operation is performed by interleaving a chip from S₁ with a chip from S₂ as shown below for C = 5:

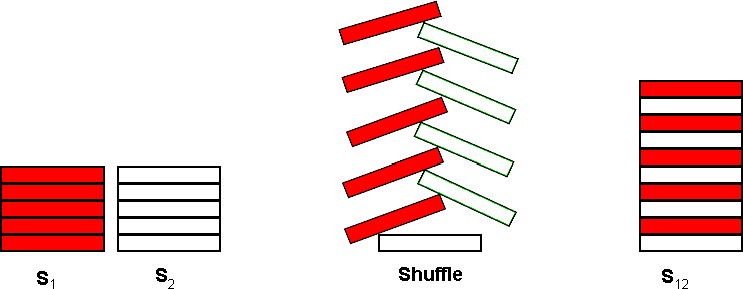
　　The single resultant stack, S₁₂, contains 2 * C chips. The bottommost chip of S₁₂ is the bottommost chip from S₂. On top of that chip, is the bottommost chip from S₁. The interleaving process continues taking the 2^nd chip from the bottom of S₂ and placing that on S₁₂, followed by the 2^nd chip from the bottom of S₁ and so on until the topmost chip from S₁ is placed on top of S₁₂.

　　After the shuffle operation, S₁₂ is split into 2 new stacks by taking the bottommost C chips from S₁₂ to form a new S₁ and the topmost C chips from S₁₂ to form a new S₂. The shuffle operation may then be repeated to form a new S₁₂.

　　For this problem, you will write a program to determine if a particular resultant stack S₁₂ can be formed by shuffling two stacks some number of times.

　　题目就是洗牌了，按照他的规则来洗，这个过程可以直接模拟，可以发现编号小于等于C（从下往上编号。）就乘以2，大于C的就乘以2然后-1，然后取模，这样的话可以看出洗牌会循环，因为只有2C种编号，对于某个来说第2C+1次一定是之前有过的编号，每一个都会循环的话，那这整个一定也会循环吧，我觉的就是周期为2C。

　　然后就是一次次洗牌就好了，出现循环的话就算是不可能了。

代码如下：

#include<iostream>
#include<cstring>

using namespace std;

char End[];
char Sta[];
int Snum[];
int C;

void change()
{
    for(int i=;i<=*C;++i)
        if(Snum[i]<=C)
            Snum[i]*=;
        else
            Snum[i]=(Snum[i]-C)*-;
}

bool judge()
{
    for(int i=;i<=C*;++i)
        if(End[Snum[i]-]!=Sta[i-])
            return ;

    return ;
}

void slove()
{
    for(int i=;i<=*C;++i)
        Snum[i]=i;

    int ans=;

    change();

    while(Snum[]!=)
    {
        if(judge())
        {
            cout<<ans<<endl;
            return;
        }

        change();
        ++ans;
    }

    if(judge())
        cout<<ans<<endl;
    else
        cout<<-<<endl;
}

int main()
{
    ios::sync_with_stdio(false);

    int T;
    char temp[];
    cin>>T;

    for(int cas=;cas<=T;++cas)
    {
        cin>>C;
        cin>>Sta;
        cin>>temp;
        strcat(Sta,temp);
        cin>>End;

        cout<<cas<<' ';
        slove();
    }

    return ;
}