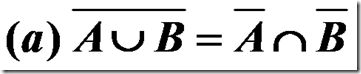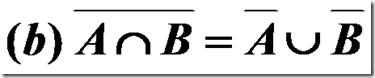组合数学：容斥原理(HDU1976)

●容斥原理所研究的问题是与若干有限集的交、并或差有关的计数.

●在实际中, 有时要计算具有某种性质的元素个数.

例：

某单位举办一个外语培训班, 开设英语, 法语两门课.设U为该单位所有人集合, A,B分别为学英语, 法语人的集合, 如图所示.

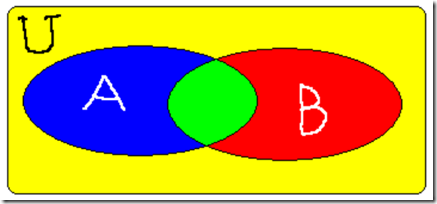
学两门外语的人数为|AB|,

只学一门外语的人数为|AB|-|AB|,

没有参加学习的人数为|U|-|AB|.

在一些计数问题中, 经常遇到间接计算一个集合中具有某种性质的元素个数比起直接计算来得简单.

例如: 计算1到700之间不能被7整除的整数个数.
先计算1到700之间能被7整除的整数个数=700/ 7=100, 所以1到700之间不能被7整除的整数个数=700-100=600.

上面举的间接计数的例子是利用了如下原理：如果A是集合S的子集, 则A中的元素个数等于S中的元素个数减去不在A中的元素个数, 这个原理可写成：

● 原理的重要推广, 称之为容斥原理,并且将它运用到若干问题上去, 其中包括：
     错位排列、
    有限制的排列、
    禁位排列和
    棋阵多项式等.

容斥原理：

DeMorgan定理：设A，B为全集U的任意两个子集，则

DeMorgan定理的推广：设A1, A2……An为U的子集，则

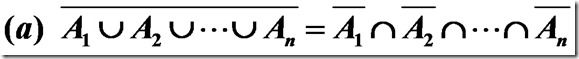
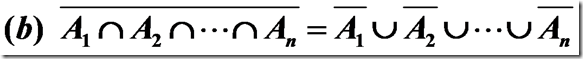
1.两个集合的容斥原理：

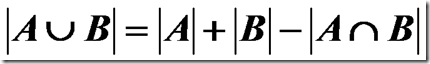
2.三个集合的容斥原理：

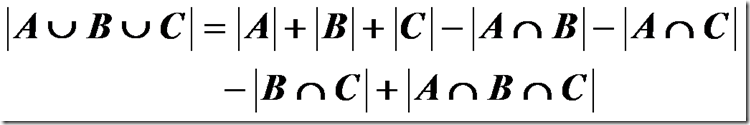
3.n个集合上的容斥原理：

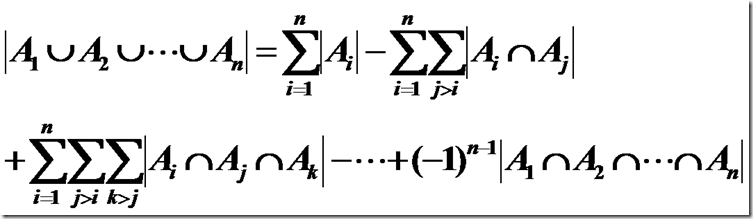
4.余集形式：

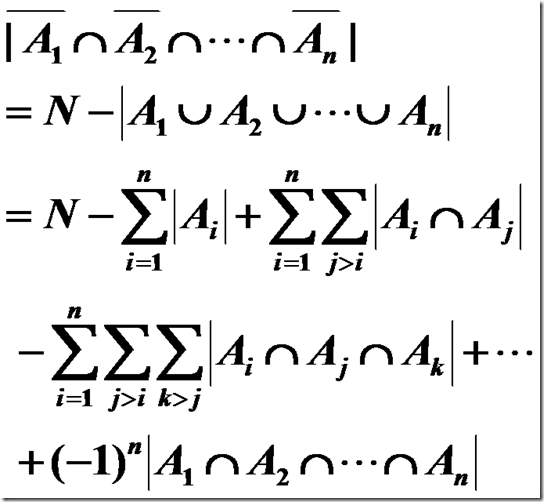
错牌问题——容斥定理的应用实例

（1..n）的错位排列个数记为Dn.  结论如下：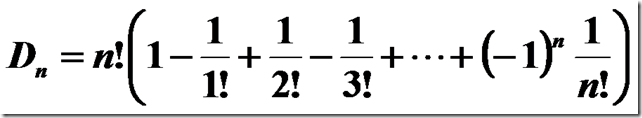

可以用容斥原理证明:
  设S={1,2,3,,n}的集合, S0为S的全排列，则s0=n! . 令Aj表示排列1,2n中使j位置上的元素恰好是j的排列的集合, j=1,2,,n. 则排列12n的所有错位排列组成集合: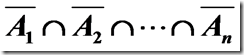

因为{1,2,3,,n}的k组合为C(n,k)个,
应用容斥原理得到:

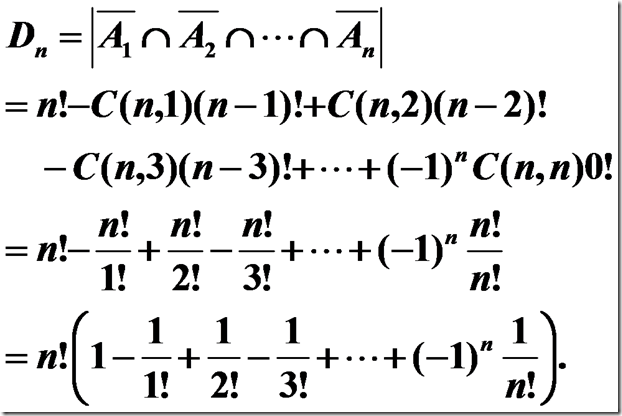
HDU1796 How many intergers can you find

How many integers can you find

Time Limit: 12000/5000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 6281    Accepted Submission(s): 1804

Problem Description

Now you get a number N, and a M-integers set, you should find out how many integers which are small than N, that they can divided exactly by any integers in the set. For example, N=12, and M-integer set is {2,3}, so there is another set {2,3,4,6,8,9,10}, all the integers of the set can be divided exactly by 2 or 3. As a result, you just output the number 7.

Input

There are a lot of cases. For each case, the first line contains two integers N and M. The follow line contains the M integers, and all of them are different from each other. 0<N<2^31,0<M<=10, and the M integer are non-negative and won’t exceed 20.

Output

For each case, output the number.

Sample Input

12 2
2 3

Sample Output

7

Author

wangye

Source

2008 “Insigma International Cup” Zhejiang Collegiate Programming Contest - Warm Up（4）

Recommend

wangye

Submit

 //**************************************************************************************************
 /*
     容斥原理的题目，并且同时包含了dfs和欧几里得算法。
 */
 //**************************************************************************************************

 #include<cstdio>
 #include<cstring>
 #include<iostream>

 using namespace std;

 const int MAXN = ;
 int p[MAXN];
 int n;
 int m;
 int Result;

 int GCD(int a, int b) { //欧几里得算法，求最大公约数。
     if (b == ) return a;
     else return GCD(b, a % b); //辗转相除。
 }

 int LCM(int a, int b) { //求最小公倍数。
     return a / GCD(a, b) * b;
 }

 int DFS(int n) { //深度优先搜索实现容斥原理。
     int i, j;
     int Cnt_Manifold; //遍历到的数的数量（数集的数量）。
     int Least_Common_Multiple; //遍历到的Cnt_Manifold个数的最小公倍数。
     Result = ; //记录每次深度搜索的结果。
     for (i = ; i < ( << m); i++) { //i的二进制位代表此次遍历查找的是那几个数
         Cnt_Manifold = ;
         Least_Common_Multiple = ; //1与任何数的最小公倍数还是那个数本身，所以初值赋为1.
         for (j = ; j < m; j++)
             if (i & ( << j)) { //筛选出要找的数并求出他们的最小公倍数。
                 Cnt_Manifold++;
                 Least_Common_Multiple = LCM(Least_Common_Multiple, p[j]);
             }
         if (Cnt_Manifold & ) { //奇数个为正偶数个为负，其作用相当于(-1)^(n - 1).
             Result += n / Least_Common_Multiple;
         }
         else {
             Result -= n / Least_Common_Multiple;
         }
     }
     return Result;
 }

 int main() {
     int cnt;
     int temp;
     while (cin >> n >> m) {
         cnt = ;
         for (int i = ; i < m; i++) {
             cin >> temp;
             if (temp) {
                 p[cnt++] = temp;
             }
         }
         m = cnt;
         cout << DFS(n - ) << endl;
     }
     return ;
 }