Robust PCA via Outlier Pursuit

引
主要结果
- 定理1
- 定理2
理论证明
- 构造Oracle Problem
算法

Xu H, Caramanis C, Sanghavi S, et al. Robust PCA via Outlier Pursuit[C]. neural information processing systems, 2010: 2496-2504.

引

这篇文章同样是关于矩阵恢复的。假设\(M = L_0 + C_0 \in \mathbb{R}^{p \times n}\)，即\(M\)实际上是由一个低秩矩阵\(L_0\)和稀疏矩阵\(C_0\)构成。需要注意的是，这里的稀疏不是指某些元素为0，而是某列为零。可以简单地认为，\(L_0\)中是一些有用的正确的样本，而\(C_0\)中的是错误的样本（非零的部分）。所以，我们能够从中将\(L_0\)的列空间恢复出来，并识别出那些样本属于\(C_0\)，即是错误的呢？

上面的作者的说法，我再用自己的话讲一下。\(M\)中的每一列都是一个\(p\)维样本，有些时候我们会遇到这种情况，有些样本是错误的。这个错误是指很严重的错误，而不是被一些噪声污染了，就像是这些数据是人的身高体重，却混入了长颈鹿的身高体重。所以呢，我们有理由相信，俩者分布在俩个子空间里，我们要做的就是判断哪个子空间里是我们想要的，哪个是错误的样本。显然正确的样本不能太少，而且正确的样本必须靠的紧凑一些。所以，这么想来，其实要求还不少。

显然直接这么做是不可靠的，举一个极端的例子：\(M\)中仅有\(M_{11}\)非零，那么显然是无法判断第一列是否是正确的样本的。所以，我们需要一个不连贯条件:

此外，作者也考虑了带噪声的问题\(M = L_0 + C_0 + N\)，其中\(N\)是噪声。

针对不带噪声的问题，作者求解的下列问题：

其中\(\|C\|_{1,2}= \sum_{i=1}^n \|C_i\|_2\)为列的\(\ell_2\)范数的和,\(\|L\|_*\)是\(L\)的核范数。

针对带噪声问题，作者求解的是下列问题：

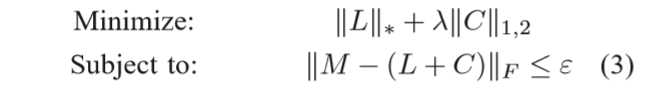
主要结果

定理1

定理2

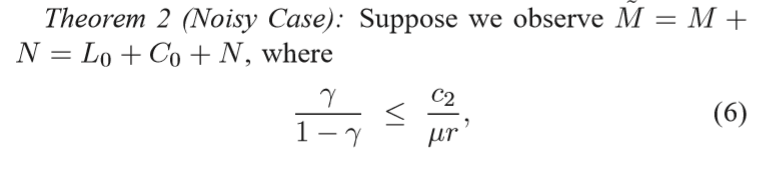
理论证明

构造Oracle Problem

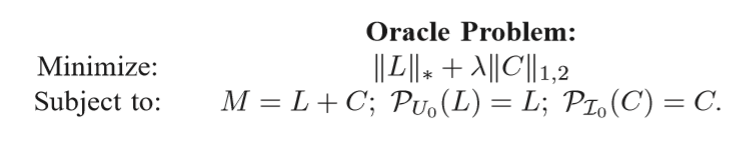
其中\(L_0 = U_0\Sigma_0V_0^T\), \(\mathcal{I}_0\)是\(C\)中不为0的非稀疏列的指标集，下面的类似的符号也类似的定义。

这个神谕问题，假设\(U_0, V_0, \mathcal{I}_0\)是已知的。

作者先证明，满足\(M=L'+C';\mathcal{P}_{U_0}(L')=L';\mathcal{P}_{\mathcal{I_0}}(C')=C'\)的解有下列性质：
\[
U'U^T = U_0U_0^T, \quad \mathcal{I'}\subseteq \mathcal{I}_0
\]
这意味着，\(\hat{L}\)的列空间和\(L_0\)的列空间一致，\(\hat{C}\)中的列（非0）也确实是错误的列。

作者再证明，对于\((L', C')\)（不要求其为Oracle Problem的最优解，可行解即可）,只要能找到一个\(Q\)满足对偶条件：

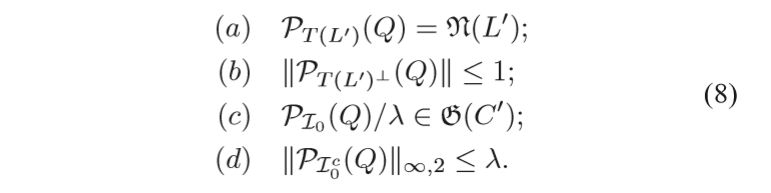
那么，\((L',C')\)也是原始问题（2）的最优解，而且如果\((b), (d)\)不等式是严格成立的，且\(\mathbb{S}_{\mathcal{I_0}}\cap \mathbb{S}_{V'} = \{0\}\)，那么\((L', C')\)将是（2）的唯一最优解。
结合上面的证明，我们可以知道，只要我们能够证明这样的\(Q\)是存在的，那么\((L', C')\)就恢复出了同一个列子空间，并识别出了部分错误的样本。

所以我们现在需要做的就是去构造这样的一\(Q\)，假设Oracle Problem的最优解为\((\hat{L}, \hat{C})\)，作者在这个解的基础上，构造一个\(Q\)。

有定理四：

其中:

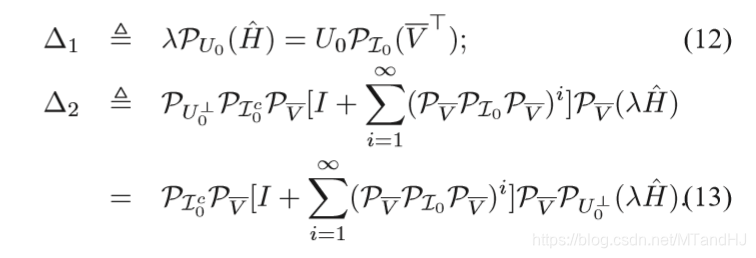
\(\bar{V} = \hat{V}\hat{U}^TU_0\)。

最后再证明定理4中的条件是能够达成的即可。

算法

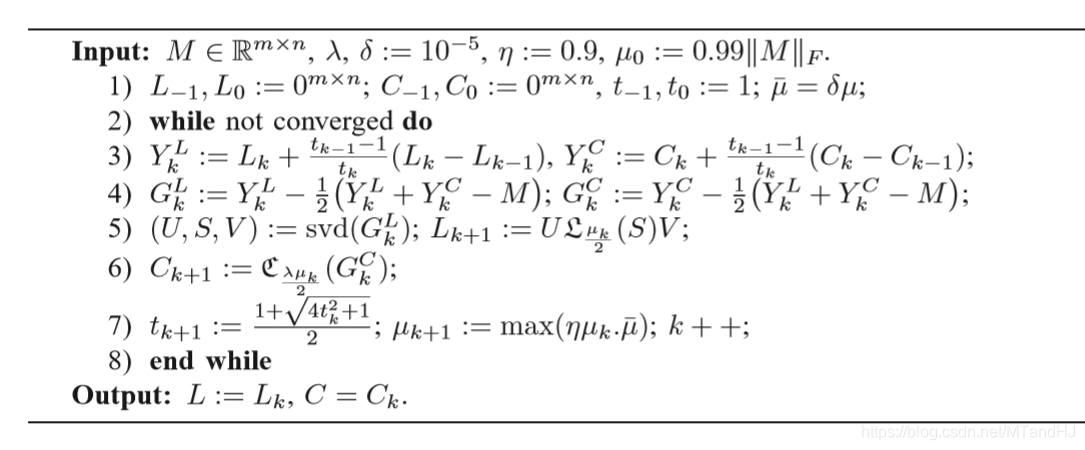
其中\(\mathfrak{L}_{\epsilon}(S)\)：如果\(S_{ii} \le \epsilon\)，截断为0，否则\(S_{ii} := S_{ii} - \epsilon \cdot sgn(S_{ii})\)。
\(\mathfrak{C}_{\epsilon}(C)\): 如果\(\|C_i\|_2 \le \epsilon\),则将整列截断为0，否则\(C_i := C_i - \epsilon C_i / \|C\|_2\)