BUUCTF-九连环
九连环
这题还是稍微有点难度的
使用16进制打开发现压缩包,用binwalk分离看看
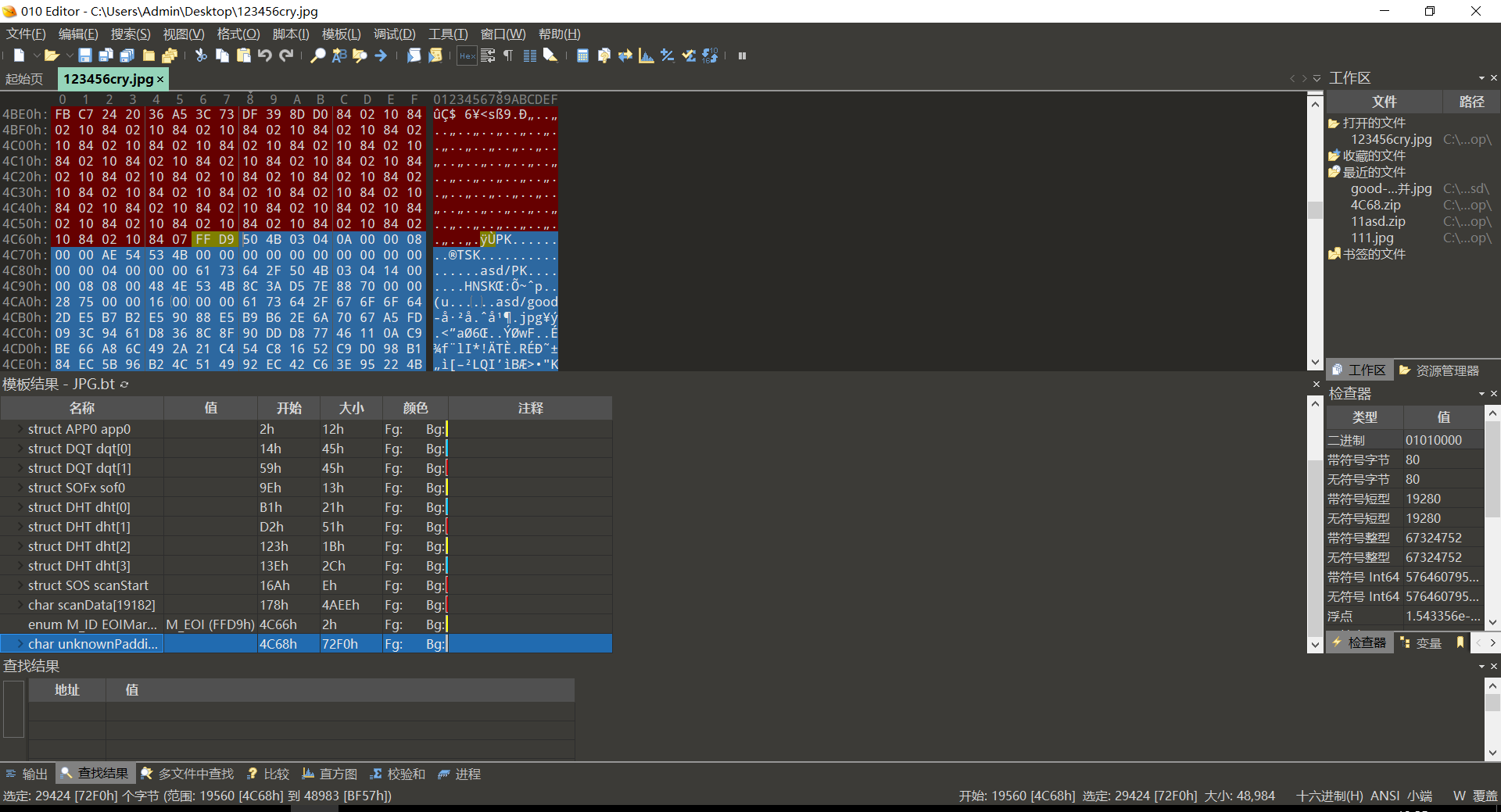
分离得到的压缩包同样16进制看看

可以发现多个压缩包,这种情况应该是伪加密的方式,但是直接使用修复压缩包的方式没法做出来。
这里有两种方式,一种是手动分离压缩包,一个是直接修改数据包16进制将加密改掉。
分离压缩包,我是简单粗暴直接从这里将下面的全部生成一个新的压缩包即可,会提示压缩包损坏,但是可以解压出来的。
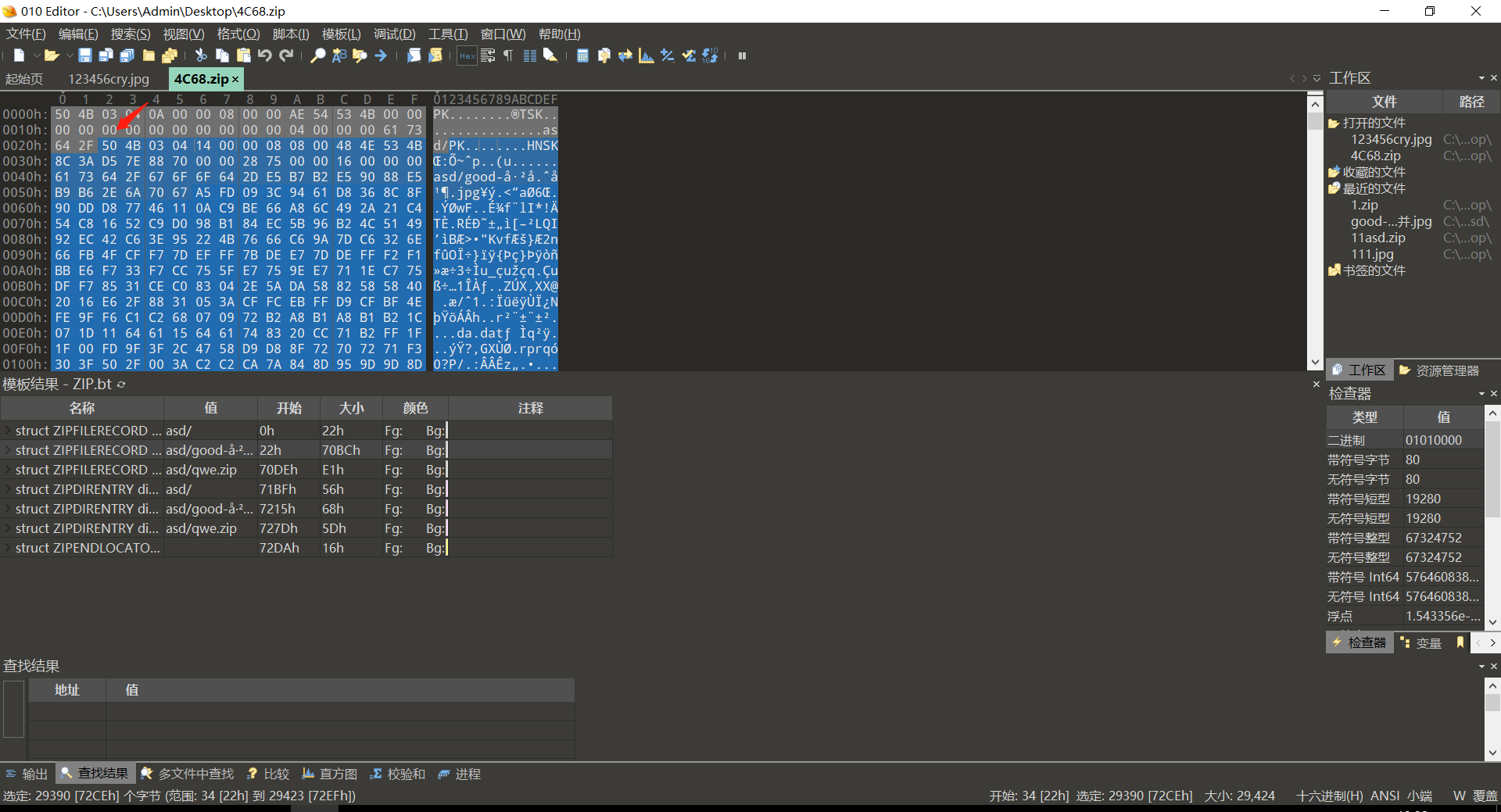
或者搜索504b0102找到这个地方,原本显示01改为00因为这个位置偶数不加密,奇数加密。同样可以解压。
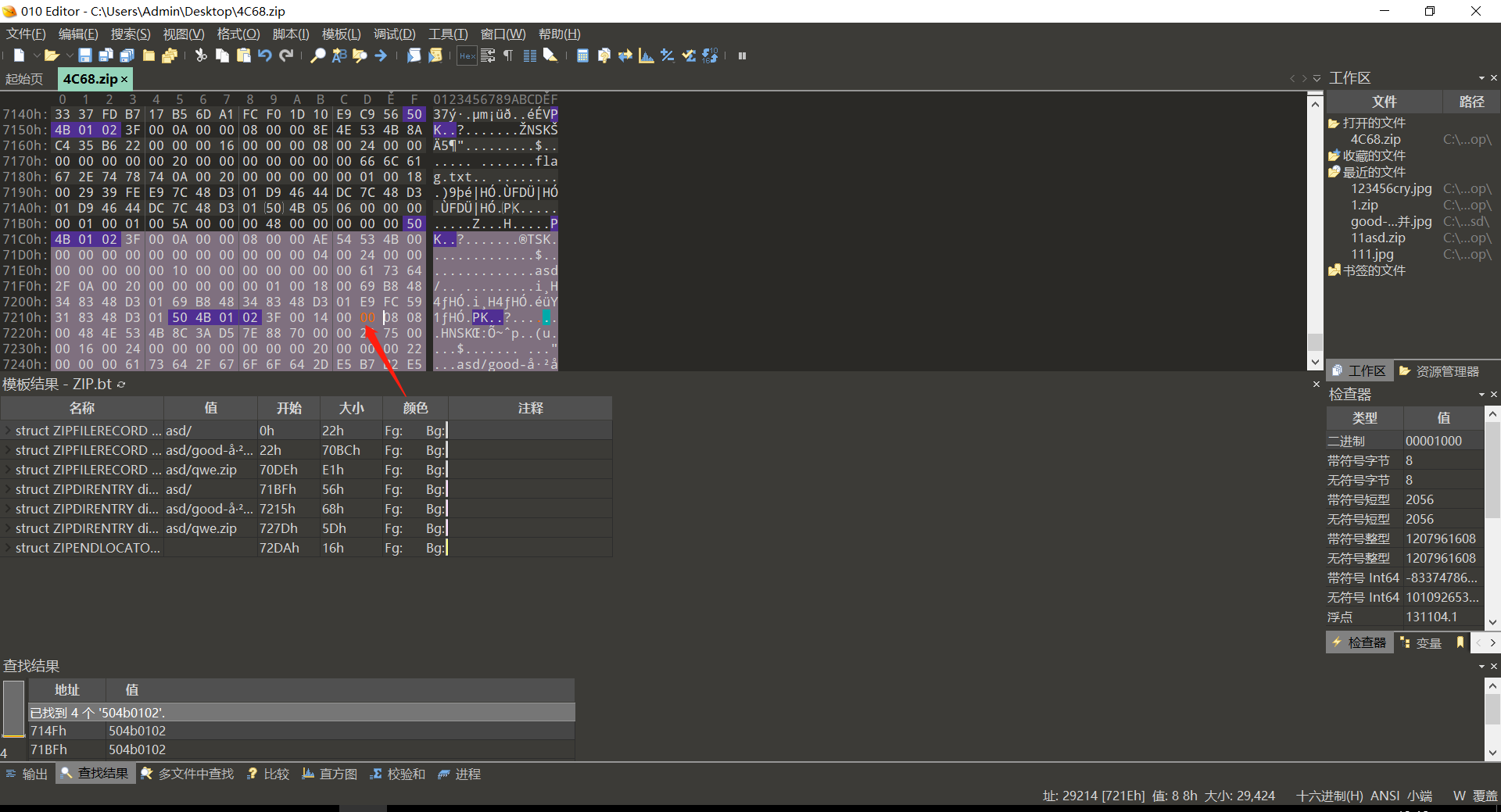
使用lsb隐写也没看到啥东西,steghide看看
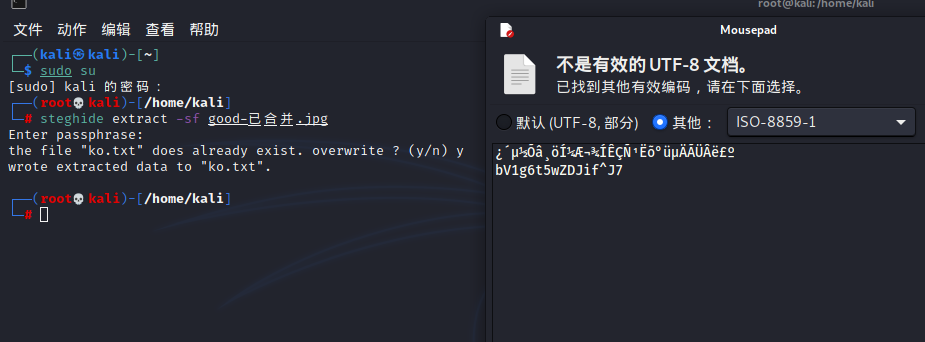
使用这个密码解压最后一个压缩包即可。
flag{1RTo8w@&4nK@z*XL}
BUUCTF-九连环的更多相关文章
- buuctf misc 刷题记录
1.金三胖 将gif分离出来. 2.N种方法解决 一个exe文件,果然打不开,在kali里分析一下:file KEY.exe,ascii text,先txt再说,base64 图片. 3.大白 crc ...
- 【杂】孔明锁6根解法 & 九连环的拆卸方法及还原
**************************** Part1: 孔明锁6根解法: **************************** 第一步,编号: 第二步,按照编号组装: 第三步,完成 ...
- asp.net 实现“九连环”小游戏
asp.net 实现"九连环"小游戏 wildcatsky(原作) public Class ChinaRing1 Inherits System.Web.UI.Page #Re ...
- 【BZOJ5300】[CQOI2018]九连环 (高精度,FFT)
[BZOJ5300][CQOI2018]九连环 (高精度,FFT) 题面 BZOJ 洛谷 题解 去这里看吧,多么好 #include<iostream> #include<cstdi ...
- CTF显隐术:九连环
题目:http://www.shiyanbar.com/ctf/2007 这个也挺基础的,需要注意的是:1.不要因为binwalk扫不出来就以为没有隐藏嵌入数据.2.千万不要暴力破解压缩包,如果是这样 ...
- # BZOJ5300 [CQOI2018]九连环 题解 | 高精度 FFT
今天做了传说中的CQOI六道板子题--有了一种自己很巨的错觉(雾 题面 求n连环的最少步数,n <= 1e5. 题解 首先--我不会玩九连环-- 通过找规律(其实是百度搜索)可知,\(n\)连环 ...
- BZOJ5300:[CQOI2018]九连环——题解
一种打表的方法,适用于知道如何解九连环的人. 我们知道,解九(n)连环必须先解第九(n)环,然后解八(n-1).七(n-2)-- 根据这个我们飞快的写出了一个递推式,设\(f[i]\)为\(i\)连环 ...
- Chinese Rings (九连环+矩阵快速幂)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2842 题目: Problem Description Dumbear likes to play th ...
- CQOI2018 九连环 打表找规律 fft快速傅里叶变换
题面: CQOI2018九连环 分析: 个人认为这道题没有什么价值,纯粹是为了考算法而考算法. 对于小数据我们可以直接爆搜打表,打表出来我们可以观察规律. f[1~10]: 1 2 5 10 21 4 ...
- 刷题记录:[BUUCTF 2018]Online Tool
目录 刷题记录:[BUUCTF 2018]Online Tool 一.知识点 1.escapeshellarg和escapeshellcmd使用不当导致rce 刷题记录:[BUUCTF 2018]On ...
随机推荐
- Python脚本----打印菜单
def print_menu(): """打印菜单""" print ("="*50) print ("1. ...
- iNeuOS工业互联网操作系统,三维(3D)模型在线编辑应用和实时数据统计(和值、均值、众数、方差、中位数等)
目 录 1. 概述... 1 2. 三维(3D)模型在线编辑与应用... 2 3. 实时数据统计... 4 1. 概述 此次,iNeuOS工业互联网操作系 ...
- 论文阅读 DynGEM: Deep Embedding Method for Dynamic Graphs
2 DynGEM: Deep Embedding Method for Dynamic Graphs link:https://arxiv.org/abs/1805.11273v1 Abstract ...
- Revit二次开发之添加选项卡和按钮
我们日常在revit开发中经常会用到按钮,可以通过revitAPI提供的接口创建按钮,今天我简单介绍一下两种按钮,一种是单命令按钮,另一种是含下拉菜单的按钮,包括创建他们的方法. 实现方法 1.实 ...
- GO语言学习——Go语言基础之流程控制一
Go语言基础之流程控制 if else(分支结构) package main import "fmt" // if条件判断 func main(){ // age := 19 // ...
- 数据库基础知识详解五:MySQL中的索引和其两种引擎、主从复制以及关系型/非关系型数据库
1.MySQL中的索引 在MySQL,索引是由B+树实现的,B+是一种与B树十分类似的数据结构. 形如下面这种: 其结构特点: (1)有n课子树的结点中含有n个关键码. (2)非根节点子节点数: ce ...
- OpenHarmony 3.1 Beta版本关键特性解析——ArkUI容器类API介绍
(以下内容来自开发者分享,不代表 OpenHarmony 项目群工作委员会观点) 刘鑫 容器类,顾名思义就是存储的类,用于存储各种数据类型的元素,并具备一系列处理数据元素的方法.在 ArkUI 开发框 ...
- B08. BootstrapBlazor实战 Menu 导航菜单使用(2)
接上篇: B08. BootstrapBlazor实战 Menu 导航菜单使用(1) 3.项目模板 节省时间,直接使用 Bootstrap Blazor App 模板快速搭建项目 传送门: https ...
- 解决vue安装less报错Failed to compile with 1 errors的问题
1.创建vue项目后安装less,执行 npm install less less-loader --save-dev 下载版本为:less-loader@6.1.0 , less@3.11.3,重启 ...
- SQL注入的几种类型
SQL注入就是: 将构造SQL语句来插入到web提交的数据之中,让其返回数据时运行自己构造的恶意SQL语句. SQL注入构造恶意SQL语句的方法有: 构造堆叠,构造闭合,构造报错,构造时间差,等等 S ...
