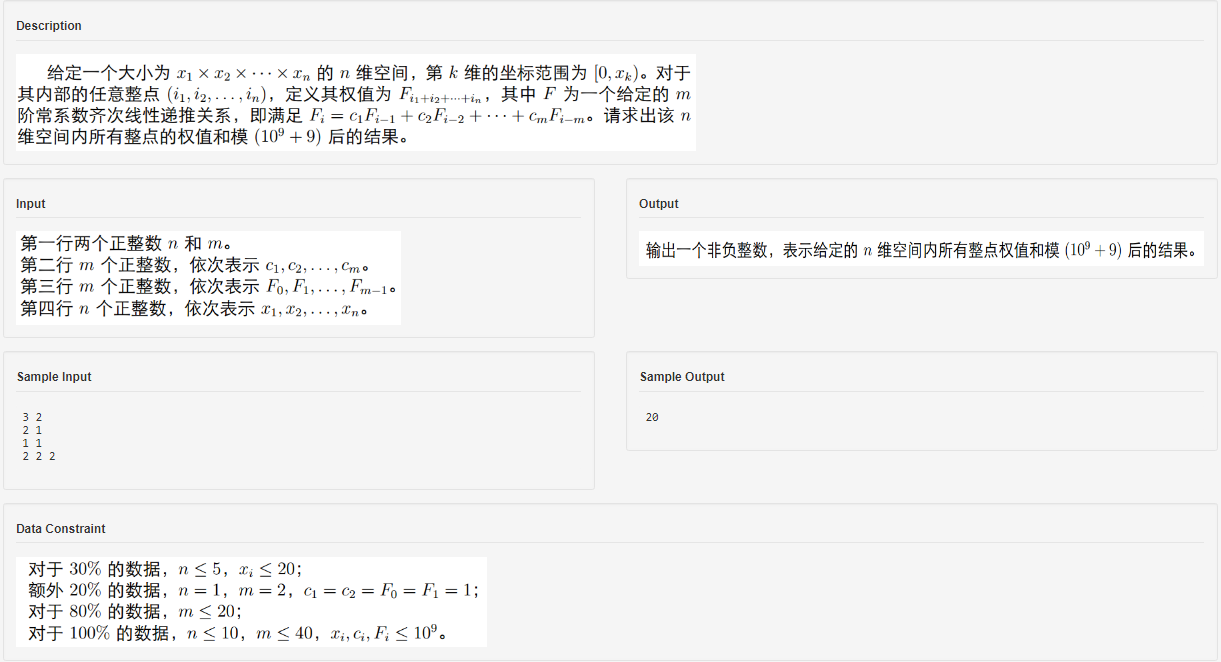
JZOJ 4276【NOIP2015模拟10.28A组】递推

【NOIP2015模拟10.28A组】递推

思路一

对于 \(30%\) 的数据，由于 \(n\) 和 \(x_i\) 都比较小，所以依题暴力枚举每个整点的坐标算贡献即可

思路二

对于额外 \(20%\) 的数据，发现 \(n=1\) 且有数列 \(F\) 为斐波那契数列，于是就变成求 \(\sum_{i=0}^{x_0 - 1}Fib_i\)

于是我们可以矩阵优化求和

思路三

既然提到矩阵，我们不妨顺着这个思路来想

如果只有一维，我们很容易用矩阵加速递推切掉它

那么考虑高维

发现唯一剩下的问题是如何计算括号中的矩阵之和

因为他们出现了等比

于是考虑暂且抛开单位矩阵 \(I\)

记 F = \(A + A^2 + A^3 + A^4 + ... + A^n\)

\(mid = \lfloor \frac{n}{2} \rfloor\)

\[F(n) =
\left \{
\begin{aligned}
(A + A^2 + A^3 + A^4 + ... + A^{mid})(A^{mid} + I) & & (\texttt{n is even}) \\
(A + A^2 + A^3 + A^4 + ... + A^{mid})(A^{mid} + I) + A^n & & (\texttt{n is odd})
\end{aligned}
\right.
\]

由于题目比较恶心，即使 \(A^n\) 用矩阵快速幂算也会 \(T\) 掉

因为快速幂和分治过程性质一样

所以我们考虑在分治的过程中算出 \(A^n\)

详见代码

\(Code\)

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
typedef long long LL;

const int N = 15 , M = 45;
const int P = 1e9 + 9;
int n , m , c[M] , f[M];
LL ans;

struct matrix{
	int m[M][M];
}A , Q , I , Now , Sum , res;

inline matrix Mul(matrix a , matrix b) //矩阵乘法
{
	memset(res.m , 0 , sizeof res.m);
	for(register int i = 1; i <= m; i++)
		for(register int j = 1; j <= m; j++)
			for(register int k = 1; k <= m; k++)
				res.m[i][j] = (res.m[i][j] + 1LL * a.m[i][k] * b.m[k][j] % P) % P;
	return res;
}

inline matrix Plus(matrix a , matrix b) //矩阵加法
{
	memset(res.m , 0 , sizeof res.m);
	for(register int i = 1; i <= m; i++)
		for(register int j = 1; j <= m; j++)
			res.m[i][j] = (a.m[i][j] + b.m[i][j]) % P;
	return res;
}

inline matrix divide(int x)
{
	if (x == 1) return Q = A;
	int mid = x >> 1;
	matrix tmp = divide(mid); //分而治之
	matrix temp;
	temp = Mul(tmp , Q);
	tmp = Plus(tmp , temp);
	Q = Mul(Q , Q); //平方算A^{2*mid}
	if (!(x & 1)) return tmp;
	Q = Mul(Q , A); //奇数时再乘个A，和快速幂同理
	tmp = Plus(tmp , Q);
	return tmp;
}

int main()
{
	freopen("recursion.in" , "r" , stdin);
	freopen("recursion.out" , "w" , stdout);
	scanf("%d%d" , &n , &m);
	for(register int i = 1; i <= m; i++) scanf("%d" , &c[i]);
	for(register int i = 0; i < m; i++) scanf("%d" , &f[i]);
	for(register int i = 1; i <= m; i++) A.m[i + 1][i] = 1 , I.m[i][i] = Sum.m[i][i] = 1;
	for(register int i = 1; i <= m; i++) A.m[i][m] = c[m - i + 1];

	int x;
	for(register int i = 1; i <= n; i++)
	{
		scanf("%d" , &x);
		Q = I;
		Now = divide(x - 1);
		for(register int j = 1; j <= m; j++) Now.m[j][j] = (Now.m[j][j] + 1) % P;  //加上单位矩阵I
		Sum = Mul(Now , Sum); //先算括号中的
	}
	for(register int i = 1; i <= m; i++) //把f乘上来
		ans = (ans + 1LL * f[i - 1] * Sum.m[i][1] % P) % P;
	printf("%lld" , ans);
}