Codeforces gym102058 J. Rising Sun-简单的计算几何+二分 (2018-2019 XIX Open Cup, Grand Prix of Korea (Division 2))

J. Rising Sun

time limit per test

1.0 s

memory limit per test

1024 MB

input

standard input

output

standard output

Joon has a midterm exam tomorrow, but he hasn't studied anything. So he decided to stay up all night to study. He promised himself that he will not stop studying before the sun rises.

Joon's house is in some mountains. For convenience, let's say that Joon is living in a 2-dimensional coordinate system. The mountains are in the region y≥0y≥0, starting at x=a0x=a0, and the boundary of them consists of 2n2n line segments parallel to either y=xy=x or y=−xy=−x.

More precisely, the boundary of the mountains can be described by (2n−1)(2n−1) additional integers, where the iith number aiai of them is the xx-coordinate of the iith cusp of the mountains. The boundary line starts at (a0,0)(a0,0), proceeds parallel to y=xy=x until its xx-coordinate reaches a1a1, then proceeds parallel to y=−xy=−x until its xx-coordinate reaches a2a2, and so on. After the last step, the line proceeds parallel to y=−xy=−x until it meets the xx-axis.

The interior of the mountains is the region below the boundary and above the xx-axis. Thus, the interior and the boundary are disjoint.

At some point between x=a0x=a0 and x=a2n−1x=a2n−1, there is Joon's house on the boundary of the mountains. The size of his house is neglectable compared to the mountains.

Currently, the sun is at the origin and it rises vertically (+y+y direction), 1 per minute. Joon can see the sun if the interior of the mountains does not intersect the straight line segment connecting Joon's house and the sun. Joon is completely exhausted and wants to know when can he stop studying. But as you may expect, he is out of his mind, so he cannot do such difficult math. Help him!

Input

The first line of the input contains an integer nn (1≤n≤1031≤n≤103).

The next line contains 2n2n integers, the iith of which is the integer ai−1ai−1 (1≤a0<⋯<a2n−1≤1061≤a0<⋯<a2n−1≤106).

The last line contains an integer xx, the xx-coordinate of Joon's house (a0≤x≤a2n−1a0≤x≤a2n−1).

It is guaranteed that the boundary of the mountains is in the region y≥0y≥0.

Output

Print exactly one integer mm, the smallest integer such that Joon can see the sun after mm minutes.

Examples

input

Copy

2
1 4 6 7
7

output

Copy

5

input

Copy

2
3 4 5 7
7

output

Copy

0

input

Copy

3
4 9 12 13 14 16
15

output

Copy

8

Note

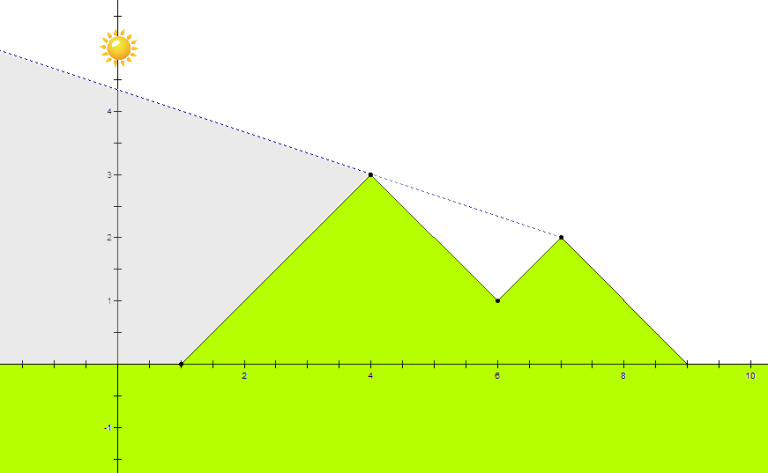
Figure: Illustration of the first example.

题意就是给你山头的横坐标x，然后山的轮廓是一个山头到另一个山头的形状是与y=x或者y=-x平行的，坐标奇数是y=x平行的，偶数是与y=-x平行的，然后给你小孩家坐标的横坐标，他家在山的轮廓线上。

太阳沿着y轴垂直上升，一分钟还是一小时(忘了)上升1米，问你他什么时候能看到太阳。

直接先算出每个山头的横坐标，然后算出来小孩家的纵坐标，然后二分太阳的高度，通过太阳的坐标和小孩家的坐标，推出来直线的方程式，然后枚举每个山头，算出高度与实际的高度比较一下就可以了。

一开始直接枚举山头算直线，最后小数上取整，没过，改了二分过的，而且二分右界一开始设的1e6，wa44，改成1e8过的。。。

题目也小小暗示了二分，因为输出的是一个整数，OK

代码:

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn=1e6+;
 const int inf=0x3f3f3f3f;

 double a[maxn],b[maxn];

 int main()
 {
     int n,pos;
     cin>>n;
     for(int i=;i<=*n;i++)
         cin>>a[i];
     cin>>pos;
     double x,y;
     double bb;
     for(int i=;i<*n;i++){
         x=a[i];y=b[i];
         if(i%!=){
             bb=y-x;
             x=a[i+];y=x+bb;b[i+]=y;
         }
         else{
             bb=y+x;
             x=a[i+];y=(-)*x+bb;b[i+]=y;
         }
     }
     x=a[*n];y=b[*n];
     bb=y+x;
     x=bb;y=;a[*n+]=x;b[*n+]=;
 //    for(int i=1;i<=2*n+1;i++){
 //        cout<<"("<<a[i]<<","<<b[i]<<")"<<endl;
 //    }
     int cnt=;
     double X=pos,Y;
     for(int i=;i<=*n+;i++){
         if(a[i]<X&&a[i+]>=X){
             cnt=i+;
             double k=(b[i]-b[i+])/(a[i]-a[i+]);
             double bb=b[i]-k*a[i];
             Y=k*X+bb;
             break;
         }
     }
     int ans=inf;
 //    for(int i=1;i<cnt;i++){
 //        double k=(Y-b[i])*1.0/(X-a[i]);
 //        double bb=Y-k*X;
 //        int flag=0;
 //        for(int i=1;i<cnt;i++){
 //            double h=k*a[i]+bb;
 //            if(h>=b[i]) continue;
 //            else{flag=1;break;}
 //        }
 //        if(flag==0) ans=min(ans,bb);
 //    }
 //    ans=ceil(ans);
 //    if(ans==-0) ans=0;
     int l=,r=1e8+;
     while(l<=r){
         int mid=(l+r)>>;
         double k=(Y-mid)/X;
         double bb=Y-k*X;
         int flag=;
         for(int i=;i<cnt;i++){
            double h=k*a[i]+bb;
            if(h>=b[i]) continue;
            else{flag=;break;}
         }
         if(flag==) r=mid-,ans=min(ans,mid);
         else l=mid+;
     }
     cout<<ans<<endl;
 }