【枚举】【尺取法】hdu6103 Kirinriki

两个等长字符串A,B的距离被定义为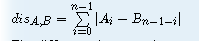

给你一个字符串，问你对于所有长度相等的不相交子串对，其距离不超过m的前提下，最长的长度是多少。

枚举对称轴，两侧先贪心地扩展到最长，超过m之后，再缩短靠近对称轴的端点，如此反复进行，每次更新答案的时候，都用的是当前“近对称轴端点”固定时的最长值。

复杂度O(n^2)。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int Abs(int x){
	return x<0 ? (-x) : x;
}
int T,m,n;
char a[5005];
int main(){
	scanf("%d",&T);
	for(;T;--T){
		int ans=0;
		scanf("%d%s",&m,a+1);
		n=strlen(a+1);
		for(int i=1;i<n;++i){
			if(i==6){
				i=6;
			}
			int sum=0;
			int p1=i,p2=i+1,q1=i,q2=i+1;
			while(p1>=1 && p2<=n){
				while(sum<=m && p1>=1 && p2<=n){
					sum+=Abs(a[p1]-a[p2]);
					if(sum<=m){
						ans=max(ans,q1-p1+1);
					}
					--p1;
					++p2;
				}
				while(sum>m){
					sum-=Abs(a[q1]-a[q2]);
					--q1;
					++q2;
					if(sum<=m){
						ans=max(ans,q1-p1);
					}
				}
			}
		}
		for(int i=2;i<n;++i){
			int sum=0;
			int p1=i-1,p2=i+1,q1=i-1,q2=i+1;
			while(p1>=1 && p2<=n){
				while(sum<=m && p1>=1 && p2<=n){
					sum+=Abs(a[p1]-a[p2]);
					if(sum<=m){
						ans=max(ans,q1-p1+1);
					}
					--p1;
					++p2;
				}
				while(sum>m){
					sum-=Abs(a[q1]-a[q2]);
					--q1;
					++q2;
					if(sum<=m){
						ans=max(ans,q1-p1);
					}
				}
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}