【占位】HihoCoder1317 跳舞链

跳舞链

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Ho最近遇到一个难题，他需要破解一个棋局。

棋局分成了n行，m列，每行有若干个棋子。小Ho需要从中选择若干行使得每一列有且恰好只有一个棋子。

比如下面这样局面：

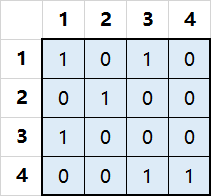
其中1表示放置有棋子的格子，0表示没有放置棋子。

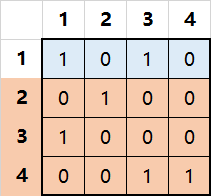
对于上面这个问题，小Ho经过多次尝试以后得到了解为选择2、3、4行就可以做到。

但是小Ho觉得自己的方法不是太好，于是他求助于小Hi。

小Hi：小Ho你是怎么做的呢？

小Ho：我想每一行都只有两种状态，选中和未被选中。那么我将选中视为1，未选中视为0。则每一种组合恰好对应了一个4位的01串，也就是一个4位的二进制数。

小Hi：恩，没错。

小Ho：然后我所做的就是去枚举每一个二进制数然后再来判定是否满足条件。

小Hi：小Ho你这个做法本身没什么问题，但是对于棋盘行数再多一点的情况就不行了。

小Ho：恩，我也这么觉得，那你有什么好方法么？

小Hi：我当然有了，你听我慢慢道来。

提示：跳舞链

输入

第1行：1个正整数t，表示数据组数，1≤t≤10。

接下来t组数据，每组的格式为：

第1行：2个正整数n,m，表示输入数据的行数和列数。2≤n,m≤100。

第2..n+1行：每行m个数，只会出现0或1。

输出

第1..t行：第i行表示第i组数据是否存在解，若存在输出"Yes"，否则输出"No"。

样例输入

2
4 4
1 1 0 1
0 1 1 0
1 0 0 0
0 1 0 1
4 4
1 0 1 0
0 1 0 0
1 0 0 0
0 0 1 1

样例输出

No
Yes

占位，等我再弄几个树的问题，就来搞DLX...高斯消元...等