【C++小白成长撸】--(续)单偶数N阶魔方矩阵
1 /*程序的版权和版本声明部分:
**Copyright(c) 2016,电子科技大学本科生
**All rights reserved.
**文件名:单偶数N阶魔方矩阵
**程序作用:单偶数N阶魔方矩阵
**作者:Amoshen
**完成日期:2016.11.2
**版本号:V1.0
*/
#include<iostream> using namespace std; #define MAX_SIZE 100 int main(void)
{
int m,u,n,ROW,CIE,ROW1,CIE1,i,j;//ROW为行,CIE为列,ROW1为临时行变量,CIE1为临时列变量,i,j分别表示行变量和列变量
int MAGIC[MAX_SIZE][MAX_SIZE] = {},b[MAX_SIZE][MAX_SIZE] = {},EX[MAX_SIZE][MAX_SIZE] = {}; cout << "请输入m,注意:n = 2*(2 * m + 1),即m输入1,得到一个6阶魔方矩阵"<<endl;
cout << "m = ";
cin >> m; n = *( * m + );
u = n/;
//先填充第一个u*u魔阵
ROW = ;
CIE = (u - )/; MAGIC[ROW][CIE] = ;
b[ROW][CIE] = ; for(i = ;i <= (u*u);i++)
{
ROW1 = ROW - ;
CIE1 = CIE + ; if(ROW1 < )
{
ROW1 = u - ;
}
if(CIE1 > (u - ))
{
CIE1 = ;
} if(b[ROW1][CIE1] == )
{
ROW = ROW1;
CIE = CIE1;
MAGIC[ROW][CIE] = i;
b[ROW][CIE] = ;
}
else
{
ROW = ROW + ;
if(ROW == u)
{
ROW = ;
}
MAGIC[ROW][CIE] = i;
b[ROW][CIE] = ;
}
}
//再填充第四个魔阵(右下角)
for(i = u;i < *u;i++)
{
for(j = u;j < *u;j++)
{
MAGIC[i][j] = MAGIC[i-u][j-u] + u*u;
}
}
//右上角
for(i = ;i < u;i++)
{
for(j = u;j < *u;j++)
{
MAGIC[i][j] = MAGIC[i+u][j] + u*u;
}
}
//左下角
for(i = u;i < *u;i++)
{
for(j = ;j < u;j++)
{
MAGIC[i][j] = MAGIC[i-u][j+u] + u*u;
}
}
//右上角与右下角的交换
for(i = ;i < u;i++)
{
for(j = *u-;j > (*u-m);j--)
{
EX[i][j] = MAGIC[i][j];
MAGIC[i][j] = MAGIC[i+u][j];
}
}
for(i = ;i < u;i++)
{
for(j = *u-;j > (*u-m);j--)
{
MAGIC[i+u][j] = EX[i][j];
}
}
//左上角与左下角的交换
for(i = ;i < u;i++)
{
if(i == (u-)/)
{
for(j = ;j <= m;j++)
{
EX[i][j] = MAGIC[i][j];
MAGIC[i][j] = MAGIC[i+u][j];
}
}
else
{
for(j = ;j < m;j++)
{
EX[i][j] = MAGIC[i][j];
MAGIC[i][j] = MAGIC[i+u][j];
}
}
}
for(i = ;i < u;i++)
{
if(i == (u-)/)
{
for(j = ;j <= m;j++)
{
MAGIC[i+u][j] = EX[i][j];
}
}
else
{
for(j = ;j < m;j++)
{
MAGIC[i+u][j] = EX[i][j];
}
}
} cout << n << "阶魔方矩阵:" <<endl; for(i = ;i < *u;i++)
{
for(j = ;j < *u;j++)
{
cout << MAGIC[i][j] <<'\t';
}
cout <<endl;
} return ;
}
原理
因为是单偶数n = 2*(2*m + 1),如果把整个魔方矩阵均分为4份,每份都是奇数阶,利用奇数阶的算法来填充。
(如图)

完成后的效果图
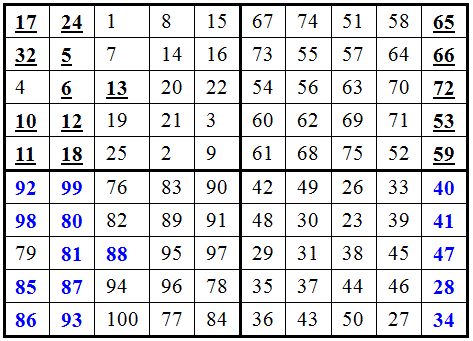
把最右边m-1列中B与C对应相交换
A的中间一行,从第二列开始,m格与对应D交换,其余从最左边开始m格与D对应交换
交换后的最终效果图
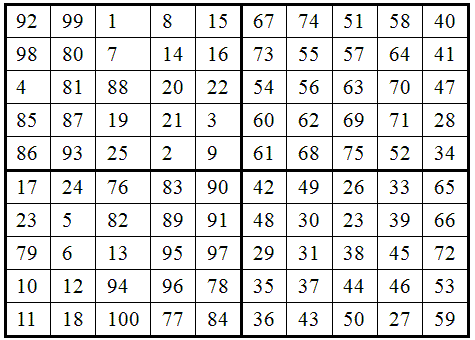
【C++小白成长撸】--(续)单偶数N阶魔方矩阵的更多相关文章
- 【C++小白成长撸】--(续)双偶数N阶魔阵
原理: 把双偶数N阶魔阵均分为(N/4)^2个4阶魔阵(4*4) 每个魔阵的对角线都标为"-1",其余位置标为"0" 从第一个位置(a[0][0])从左到右,从 ...
- 【C++小白成长撸】--N阶幻方(魔阵)矩阵
解决方法:1.第一个元素放在第一行中间一列 2.下一个元素存放在当前元素的上一行.下一列. 3.如果上一行.下一列已经有内容,则下一个元素的存放位置为当前列的下一行. 在找上一行.下一行或者下一列的时 ...
- 【C++小白成长撸】--矩阵乘法程序
矩阵乘法是大学矩阵课程中,相比矩阵加减法比较困难的部分. 矩阵乘法的原理: 矩阵乘法在代码中实现 得到目标矩阵的一个元素,涉及两个求和符号,一个求和符号一个for循环,两个求和符号两个for循环,再加 ...
- 【ACM小白成长撸】--贪婪法解硬币找零问题
question:假设有一种货币,它有面值为1分.2分.5分和1角的硬币,最少需要多少个硬币来找出K分钱的零钱.按照贪婪法的思想,需要不断地使用面值最大的硬币.如果找零的值小于最大的硬币值,则尝试第二 ...
- 【小白成长撸】--Fibonacci
/*程序的版权和版本声明部分: *Copyright(c) 2016,电子科技大学本科生 *All rights reserved. *文件名:Fibonacci *程序作用:计算菲薄拉稀数列 *作者 ...
- 【ACM小白成长撸】--计算单词个数
我判断单词个数的方法,根据空格‘ ’的个数 分情况 当没有单词的时候 判断第一个符号,即a[0] == ‘\0’时,赋值给存储个数的数组 当遇到空格时,只有前面一个字符不是空格字符,后面一个字符不是空 ...
- 【小白成长撸】--多项式求圆周率PI
/*程序的版权和版本声明部分: *Copyright(c) 2016,电子科技大学本科生 *All rights reserved. *文件名:多项式求PI *程序作用:计算圆周率PI *作者:Amo ...
- 【小白成长撸】--链栈(C语言版)
// 链栈.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" #include <stdio.h> #include <st ...
- 【小白成长撸】--顺序栈(C语言版)
// 顺序栈.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h"//test1.0--栈表仅限Int类型 #include <stdio. ...
随机推荐
- 阿里消息队列中间件 RocketMQ源码解析:Message发送&接收
- 最小生成树详解 prim+ kruskal代码模板
最小生成树概念: 一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边. 最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里 ...
- whatwg-fetch源码分析
fetch 是什么 XMLHttpRequest的最新替代技术 fetch优点 接口更简单.简洁,更加语义化 基于promise,更加好的流程化控制,可以不断then把参数传递,外加 async/aw ...
- Kaggle竞赛 —— 泰坦尼克号(Titanic)
完整代码见kaggle kernel 或 NbViewer 比赛页面:https://www.kaggle.com/c/titanic Titanic大概是kaggle上最受欢迎的项目了,有7000多 ...
- 常用 Http 的请求方法
第一次用markdown写博客,体验下 因为常用Http的几种请求方式,总结一下. 1.封装两个Http的最常用方法,叫做HttpHelper类. HttpPost: public static st ...
- Hadoop 之 NameNode 元数据原理
在对NameNode节点进行格式化时,调用了FSImage的saveFSImage()方法和FSEditLog.createEditLogFile()存储当前的元数据.Namenode主要维护两个文件 ...
- 微信小程序简单入门1
参考文档:https://mp.weixin.qq.com/debug/wxadoc/dev/index.html 1 创建项目 开发者工具安装完成后,打开并使用微信扫码登录.选择创建"项 ...
- python学习之元组与文件
元组 元组是最后一个python集合类型.元组由简单的对象构成,元组与列表非常相似,只不过元组不能在原处修改,并且通常写成圆括号,虽然元组部支持任何方法调用,但元组具有列表的大多数属性. 实际应用中的 ...
- MySQL主从失败 错误Got fatal error 1236解决方法
--MySQL主从失败 错误Got fatal error 1236解决方法 ----------------------------------------------------2014/05/1 ...
- leetcode 总结part1
从十月份开始到现在,差不多近3个月时间吧. 中间有的时候有事没有办法刷题,也有的题目比较难,比较麻烦,会浪费很多时间,71道题,也都是简单的. 下图是最后20道刷题的记录吧. 完成自己的目标是轻松的. ...
