hihocoder #1394 : 网络流四·最小路径覆盖（最小路径覆盖）

#1394 : 网络流四·最小路径覆盖

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

国庆期间正是旅游和游玩的高峰期。

小Hi和小Ho的学习小组为了研究课题，决定趁此机会派出若干个调查团去沿途查看一下H市内各个景点的游客情况。

H市一共有N个旅游景点(编号1..N)，由M条单向游览路线连接。在一个景点游览完后，可以顺着游览线路前往下一个景点。

为了避免游客重复游览同一个景点，游览线路保证是没有环路的。

每一个调查团可以从任意一个景点出发，沿着计划好的游览线路依次调查，到达终点后再返回。每个景点只会有一个调查团经过，不会重复调查。

举个例子：

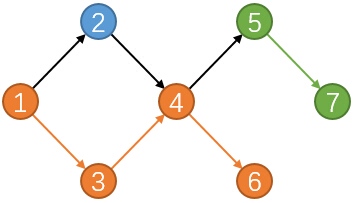
上图中一共派出了3个调查团：

1. 蓝色：调查景点；2

2. 橙色：调查景点；1->3->4->6

3. 绿色：调查景点；5->7

当然对于这个图还有其他的规划方式，但是最少也需要3个调查团。

由于小组内的人数有限，所以大家希望调查团的数量尽可能少，同时也要将所有的景点都进行调查。

当然，如何规划调查团线路的任务落到了小Hi和小Ho的头上。

提示：最小路径覆盖

输入

第1行：2个整数N,M。1≤N≤500,0≤M≤20,000。

第2..M+1行：2个数字u,v，表示一条有向边(u,v)。保证不会出现重复的边，且不存在环。

输出

第1行：1个整数，表示最少需要的调查团数量。

样例输入

7 7
1 2
1 3
2 4
3 4
4 5
4 6
5 7

样例输出

3

分析

最小路径覆盖=N-最大匹配数

code

 #include<cstdio>
 #include<algorithm>
 #include<cstring>

 using namespace std;
 const int N = ;
 const int INF = 1e9;
 struct Edge{
     int to,nxt,c;
     Edge() {}
     Edge(int x,int y,int z) {to = x,c = y,nxt = z;}
 }e[];
 int q[],L,R,S,T,tot = ;
 int dis[N],cur[N],head[N];

 inline char nc() {
     static char buf[],*p1 = buf,*p2 = buf;
     return p1==p2&&(p2=(p1=buf)+fread(buf,,,stdin),p1==p2) ? EOF :*p1++;
 }
 inline int read() {
     int x = ,f = ;char ch=nc();
     for (; ch<''||ch>''; ch=nc()) if(ch=='-')f=-;
     for (; ch>=''&&ch<=''; ch=nc()) x=x*+ch-'';
     return x*f;
 }
 void add_edge(int u,int v,int c) {
     e[++tot] = Edge(v,c,head[u]);head[u] = tot;
     e[++tot] = Edge(u,,head[v]);head[v] = tot;
 }
 bool bfs() {
     for (int i=; i<=T; ++i) cur[i] = head[i],dis[i] = -;
     L = ,R = ;
     q[++R] = S;dis[S] = ;
     while (L <= R) {
         int u = q[L++];
         for (int i=head[u]; i; i=e[i].nxt) {
             int v = e[i].to;
             if (dis[v] == - && e[i].c > ) {
                 dis[v] = dis[u]+;q[++R] = v;
                 if (v==T) return true;
             }
         }
     }
     return false;
 }
 int dfs(int u,int flow) {
     if (u==T) return flow;
     int used = ;
     for (int &i=cur[u]; i; i=e[i].nxt) {
         int v = e[i].to;
         if (dis[v] == dis[u] +  && e[i].c > ) {
             int tmp = dfs(v,min(flow-used,e[i].c));
             if (tmp > ) {
                 e[i].c -= tmp;e[i^].c += tmp;
                 used += tmp;
                 if (used == flow) break;
             }
         }
     }
     if (used != flow) dis[u] = -;
     return used;
 }
 int dinic() {
     int ret = ;
     while (bfs()) ret += dfs(S,INF);
     return ret;
 }

 int main() {
     int n = read(),m = read();
     S = n + n + ,T = n + n + ;
     for (int i=; i<=n; ++i) add_edge(S,i,),add_edge(i+n,T,);
     for (int i=; i<=m; ++i) {
         int u = read(),v = read();
         add_edge(u,v+n,);
     }
     int ans = dinic();
     printf("%d",n-ans);
     return ;
 }