[Math Review] Statistics Basic: Sampling Distribution

Inferential Statistics

Generalizing from a sample to a population that involves determining how far sample statistics are likely to vary from each other and from the population parameter.

Sampling Distribution

The sampling distribution of a statistic is the distribution of that statistic, considered as a random variable, when derived from a random sample of size .

• Every statistic has a sampling distribution.
• There is a sampling distribution for various sample sizes.

Two Conceptualization of Sampling Distribution

• The distribution of the statistic for all possible samples from the same population of a given sample size.
• Relative frequency distribution: Consider a given size of observations are sampled and the statistic is computed and recorded. Then the process is repeated again and again. After thousands of samples are taken and the statistic computed for each, a relative frequency distribution is drawn.

The relative frequency distribution approaches the sampling distribution as the number of samples approaches infinity.

Standard Error

The most common measure of how much sample statistics differ from each other is the standard deviation of the sampling distribution of the statistic. This standard deviation is called the standard error of the statistic.

Sampling Distribution of the Mean

Mean

The mean of the sampling distribution of the mean is the mean of the population from which the scores were sampled.

 

Variance

The variance of the sampling distribution of the mean is computed as follows:

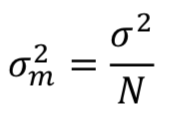
The larger the sample size, the smaller the variance of the sampling distribution of the mean.

Standard Error

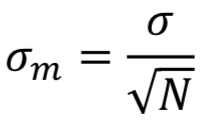
Central Limit Theorem

Given a population with a finite mean μ and a finite non-zero variance σ², the sampling distribution of the mean approaches a normal distribution  with a mean of μ and a variance of σ²/N as N, the sample size, increases.