P4342 [IOI1998]Polygon

题意翻译

题目可能有些许修改，但大意一致

多边形是一个玩家在一个有n个顶点的多边形上的游戏，如图所示，其中n＝4。每个顶点用整数标记，每个边用符号+（加）或符号*（乘积）标记。

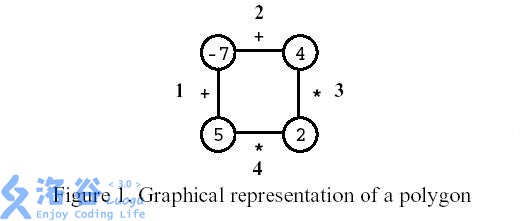
第一步，删除其中一条边。随后每一步：

选择一条边连接的两个顶点V1和V2，用边上的运算符计算V1和V2得到的结果来替换这两个顶点。

游戏结束时，只有一个顶点，没有多余的边。

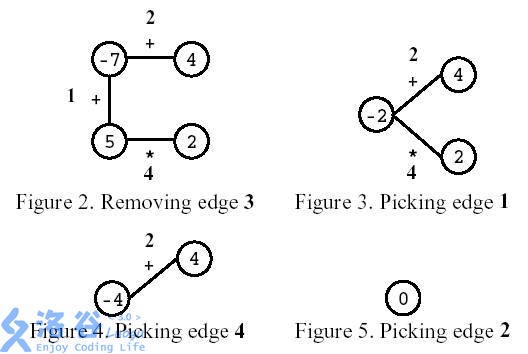
如图所示，玩家先移除编号为3的边。之后，玩家选择计算编号为1的边，然后计算编号为4的边，最后，计算编号为2的边。结果是0。

（翻译者友情提示：这里每条边的运算符旁边的数字为边的编号，不拿来计算）

编写一个程序，给定一个多边形，计算最高可能的分数。

输入格式

输入描述一个有n个顶点的多边形，它包含两行。第一行是数字n，为总边数。

第二行描述这个多边形，一共有2n个读入，每两个读入中第一个是字符，第二个是数字。

第一个字符为第一条边的计算符号(t代表相加，x代表相乘)，第二个代表顶点上的数字。首尾相连。

3 < = n < = 50

对于任何一系列的操作，顶点数字都在[-32768,32767]的范围内。

输出格式

第一行，输出最高的分数。在第二行，它必须写出所有可能的被清除后的边仍能得到最高得分的列表，必须严格递增。

感谢@2016c01 提供的翻译

题目描述

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.

On the first move, one of the edges is removed. Subsequent moves involve the following steps: �pick an edge E and the two vertices V1 and V2 that are linked by E; and �replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2. The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.

输入输出格式

输入格式：

Your program is to read from standard input. The input
describes a polygon with N vertices. It contains two lines. On the first
line is the number N. The second line contains the labels of edges 1,
..., N, interleaved with the vertices' labels (first that of the vertex
between edges 1 and 2, then that of the vertex between edges 2 and 3,
and so on, until that of the vertex between edges N and 1), all
separated by one space. An edge label is either the letter t
(representing +) or the letter x (representing *).

3 <= N <= 50

For any sequence of moves, vertex labels are in the range [-32768,32767].

输出格式：

Your program is to write to standard output. On the first line
your program must write the highest score one can get for the input
polygon. On the second line it must write the list of all edges that, if
removed on the first move, can lead to a game with that score. Edges
must be written in increasing order, separated by one space.

输入输出样例

输入样例#1：

4
t -7 t 4 x 2 x 5

输出样例#1：

33
1 2

Solution：

　　吐槽：循环时区间范围忘了乘$2$，卡了我好久好久啊`！～～～

　　很容易由题意想到要破环成链，然后想到用区间$DP$，定义状态$f[i][j]$表示区间$[i,j]$之间能计算出的最大值。

　　但是由于有乘法存在，这样很显然有后效性（因为区间$f[i,j]$的最大值有可能是由两个为负的最小值$f[i,k]*f[k+1,j]$得来），而加法显然不存在这种情况（只可能是最大值转移而来）。

　　于是，我们多定义一个状态存一段区间能计算出的最小值就好了。又由于本题是个环，所以我们直接倍长原序列。

　　设$f1[i][j]$表示区间$[i,j]$能计算出的最大值，$f2[i][j]$表示$[i,j]$能计算出的最小值，初始状态$f1[i][i]=f1[i+n][i+n]=f2[i][i]=f2[i+n][i+n]=x,i\in[1,n]$表示每个数不计算的值就是其本身，其余的$f1$赋值为$-inf$、$f2$赋值为$inf$。

　　考虑符号为$*$时（加法就正常转移$f1[i][j]$取$max$，$f2[i][j]$取$min$，就不多赘述了）：

　　最大值有两种情况：由两段区间的最大值乘积转移过来，或者两段区间的最小值乘积转移。

　　最小值有两种情况：由第一段区间最大值和第二段区间最小值转移，或者由第一段区间最小值和第二段区间最大值转移过来。

　　所以不难得到符号为$*$的状态转移方程：

　　$f1[i][j]=max(f1[i][j],max(f1[i][k]*f1[k+1][j],f2[i][k]*f2[k+1][j]))$

　　$f2[i][j]=min(f2[i][j],min(f2[i][k]*f1[k+1][j],f1[i][k]*f2[k+1][j]))$

　　目标状态为$f1[i][i+n-1],i\in[1,n]$中的$max$值。

代码：

#include<bits/stdc++.h>
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)>(b)?(b):(a))
using namespace std;
const int N=;
int n,x,f1[N][N],f2[N][N],ans=-;
bool pd[N];
char s;
int main(){
    ios::sync_with_stdio();
    cin>>n;
    memset(f1,-0x3f,sizeof f1);
    memset(f2,0x3f,sizeof f2);
    For(i,,n){
        cin>>s>>x;
        if(s=='x')pd[i]=pd[i+n]=;
        f1[i][i]=f1[i+n][i+n]=f2[i][i]=f2[i+n][i+n]=x;
    }
    For(i,,n-) For(l,,n<<){
        if(l+i>*n)break;
        int r=l+i;
        For(k,l,r-)
            if(!pd[k+]){
                f1[l][r]=Max(f1[l][r],f1[l][k]+f1[k+][r]);
                f2[l][r]=Min(f2[l][r],f2[l][k]+f2[k+][r]);
            }
            else {
                f1[l][r]=Max(f1[l][r],Max(f1[l][k]*f1[k+][r],f2[l][k]*f2[k+][r]));
                f2[l][r]=Min(f2[l][r],Min(f1[l][k]*f2[k+][r],f2[l][k]*f1[k+][r]));
            }
    }
    For(i,,n)ans=Max(f1[i][i+n-],ans);
    cout<<ans<<endl;
    For(i,,n)if(f1[i][i+n-]==ans)cout<<i<<' ';
    return ;
}