NOIP模拟 Pyramid - 斜率优化DP

题目大意：

给一个金字塔图（下面的宽度大于等于上面的宽度），每层的高度为1，从中选取k个互不重叠的矩形，使面积最大。

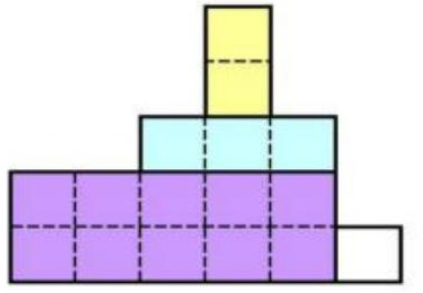
题目分析：

\(f[i][j]\)表示选到第i层，选择了j个矩形的最优方案。

转移方程：$$f[i][k] = max{f[j][k - 1] + (i - j) * (y[i] - x[i] + 1)}$$

列式并化简为斜率形式：$$S(i, j) = \frac{f[i] - f[j]}{i - j} >= y[i] - x[i] + 1$$

斜率dp裸题。

code

#include<bits/stdc++.h>
using namespace std;
const int N = 20050, K = 150;
int n, k, x[N], y[N];
typedef long long ll;
ll f[N][K];
int que[N * 2];
ll tmp[N];

inline ll calc(int i, int j){
	return tmp[j] + 1ll*(i - j) * (y[i] - x[i] + 1);
}

inline bool slopeCheck(int i, int j, int k){
	return (tmp[i] - tmp[j]) * (j - k) >=
		   (tmp[j] - tmp[k]) * (i - j);
}

int main(){
	freopen("h.in", "r", stdin);
	scanf("%d%d", &n, &k);
	for(int i = 1; i <= n; i++) scanf("%d%d", &x[i], &y[i]);

	for(int i = 1; i <= k; i++){
		int head, tail;
		que[head = tail = 1] = 0;

		for(int j = 1; j <= n; j++) tmp[j] = f[j][i - 1];
		for(int j = 1; j <= n; j++){
			while(head + 1 <= tail && calc(j, que[head]) <= calc(j, que[head + 1])) head++;
			f[j][i] = calc(j, que[head]);
			while(head <= tail - 1 && slopeCheck(j, que[tail], que[tail - 1])) tail--;
			que[++tail] = j;
		}

	}

	ll ans = 0;
	for(int i = 1; i <= n; i++) ans = max(ans, f[i][k]);
	printf("%lld", ans);
}