[HNOI2008] GT考试(DP+矩阵快速幂+KMP)

题目链接:https://www.luogu.org/problemnew/show/P3193#sub

题目描述

阿申准备报名参加 GT 考试，准考证号为 N 位数 X1,X2…Xn(0 <= Xi <= 9) ，他不希望准考证号上出现不吉利的数字。 他的不吉利数学 A1​,A2​…Am​(0≤Ai​≤9) 有 M 位，不出现是指 X1​,X2​…Xn​ 中没有恰好一段等于 A1​,A2​…Am​ ，A1​

输入输出格式

输入格式：

第一行输入N,M,K.接下来一行输入M位的数。

输出格式：

阿申想知道不出现不吉利数字的号码有多少种，输出模 K 取余的结果。

输入输出样例

输入样例#1：

4 3 100
111

输出样例#1：

81

说明

N≤109,M≤20,K≤1000

题目大意，给定长为m的子串，统计长度为n的不包含该子串的串的方案数

考虑DP解决，f[i][j]表示长串匹配到第 i 位，短串最多可以匹配到第 j 位的方案数（即表示长度为i的长串，最后j个可以匹配短串前j位的方案数）

状态转移方程如下：

f[i+1][j]=f[i][k]*g[j][k](0<=k<m)

最终答案就是∑^​f[n][i](0<=i<m)（这显然正确，仔细想想就发现这些i代表的状态互相独立，且并集包含了所有的状态）

g[i][j]表示对于短串，原本匹配了i位，匹配下一位时匹配到第j位的这个下一位的方案数

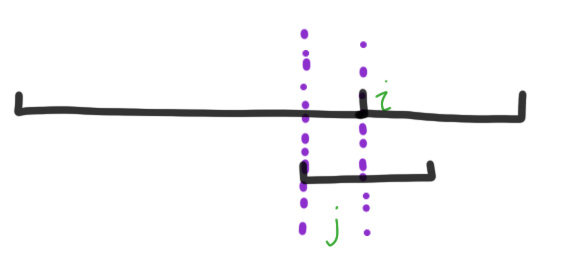
图一，短串匹配了j位，长串匹配到了i位

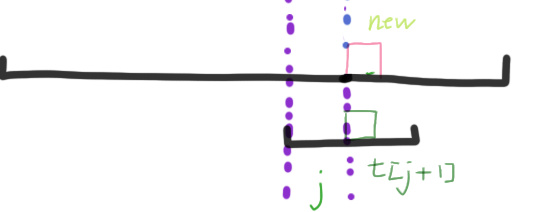
图2，长串继续向下匹配，短串失配

图3，短串转移到下一个可以匹配的地方

注意由于new是我们任意填的，因此我们只需考虑短串的下一个匹配的位置，即KMP算法中的next数组

上面三幅图实际上就是匹配的过程，是为了让读者更好的理解g数组的含义

下面我们考虑怎么求g数组。回顾g数组的含义，我们发现实际上只和短串有关（上面说了，new是任意填的）。KMP预处理出g数组，若我原来匹配了i位，枚举下一个数字，不断转移next数组直到匹配成功，最终得到一个可以匹配的位置k，然后我们让f[i][k]++统计方案数

发现n的取值过大且上述状态转移方程可用矩阵快速幂优化。注意每次乘上转移矩阵得到的矩阵存储的实际上是状态，因此其实矩阵的宽都是1来着。

考虑到每次我们转移的矩阵g是不变的，于是我们可以很快结束这个问题

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

const int N=;
int n,m,mod;
int next[N],a[N];
char s[N];
struct matrix
{
    int r,c,num[N][N];//矩阵的长宽
    matrix(){memset(num,,sizeof(num));}
    void init()
    {
        for (int i=;i<N;i++)
            num[i][i]=;
    }
}g,A;
matrix mul(matrix a,matrix b)
{
    matrix ans;
    ans.r=a.r;ans.c=b.c;
    for (int i=;i<=a.r;i++)
        for (int j=;j<=b.c;j++)
        {
            ans.num[i][j]=;
            for (int k=;k<=ans.c;k++)
            ans.num[i][j]=(ans.num[i][j]+a.num[i][k]*b.num[k][j])%mod;
        }
    return ans;
}
matrix qpow(matrix a,int x)
{
    matrix ans;
    ans.init();
    for (;x;x>>=,a=mul(a,a)) if (x&) ans=mul(ans,a);
    return ans;
}
int main()
{
    scanf("%d%d%d",&n,&m,&mod);
    scanf("%s",s);
    for (int i=;i<m;i++) a[i]=s[i]-'';a[m]=0x3f3f3f3f;
    for (int i=,j=;i<m;i++)//计算出next数组
    {
        while (j&&(a[i]!=a[j])) j=next[j];
        j+=(a[i]==a[j]);
        next[i+]=j;
    }
    for (int i=;i<m;i++)
        for (int j=;j<;j++)//预处理出g数组
        {
            int k=i;
            while (k&&a[k]!=j) k=next[k];
            k+=(a[k]==j);
            if (k<m) g.num[i][k]++;//i位可以转移到k位
        }
    A.num[][]=;A.r=;g.c=g.r=A.c=m-;//初始化
    A=mul(A,qpow(g,n));
    int ans=;
    for (int i=;i<m;i++) {ans+=A.num[][i];ans%=mod;}//统计每个状态的答案
    printf("%d",ans);
    return ;
}