UVA11694-Gokigen Naname（DFS进阶）

Problem UVA11694-Gokigen Naname

Accept: 76   Submit: 586
Time Limit: 10000 mSec

Problem Description

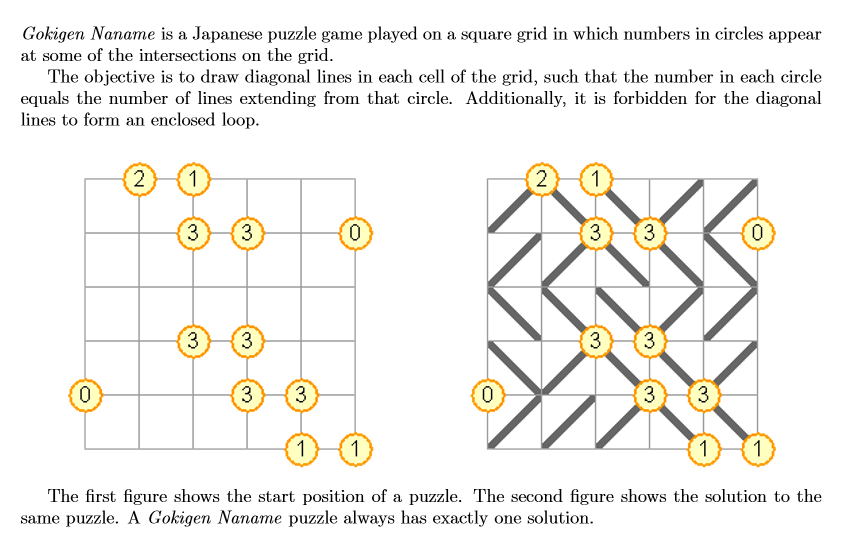
Input

The first line of the input file contains an integer N (N < 25) which denotes the total number of test cases. The description of each test case is given below: The first line of each test case contains a single integer n (2 ≤ n ≤ 7), the number of cells along each of the sides in the square grid. Then follow n+1 lines containing the contents of the intersections of the grid cells. Each such line will contain a string of n + 1 characters, either a digit between 0 and 4, inclusive, or a period (‘.’) indicating that there is no number at this intersection (arbitrarily many lines may connect to it).

 Output

For each test case print n lines, each line containing exactly n characters. Each character should either be a slash or a backslash, denoting how the corresponding grid cell is filled.

 

 Sample Input

2
3
1.1.
...0
.3..
..2.
5
.21...
..33.0
......
..33..
0..33.
....11

 

 Sample Output

\//
\\\
/\/
/\\//
//\\\
\\\//
\/\\/
///\\

题解：我感觉这个题挺难的，DFS的思路还比较直接，但是维护哪些东西比较迷茫。首先肯定有一个原图，然后要维护一下各点目前已经连了几条边，最关键的是要维护每个节点最多还能连几条边（用于剪枝）。判环的问题丢给并查集。DFS的时候从上到下，从左到右，每次连一条边更新维护的东西，要更新的东西比较多，回溯的时候别漏了。这里的并查集有必要提一句，这里不能路径压缩，因为回溯时是一种类似删除节点的操作，简单画个图就能发现如果只在回溯时修改当前节点的父节点为原来的父节点是不对的。因此这里不路径压缩，并查集基本上就是个链表的作用。剪枝有两个：1、如果一个节点连出的边数超了肯定要剪枝。2、利用lim数组，预估在最多的情况下能连几条边，如果少于目标边数，剪枝。

 #include <bits/stdc++.h>

 using namespace std;

 const int maxn = ;

 int n;
 int gra[maxn][maxn], lim[maxn][maxn];
 int cur[maxn][maxn], ans[maxn][maxn];
 int dx[] = { ,,, };
 int dy[] = { ,,, };

 int pre[maxn*maxn];

 int findn(int x) {
     return x == pre[x] ? x : findn(pre[x]);
 }

 inline bool ok(int x, int y) {
     if (gra[x][y] == -) return true;
     if (cur[x][y] <= gra[x][y] && cur[x][y] + lim[x][y] >= gra[x][y]) return true;
     return false;
 }

 bool dfs(int x, int y) {
     if (y == n) x++, y = ;
     if (x == n) return true;

     cur[x][y]++, cur[x + ][y + ]++;
     lim[x][y]--, lim[x + ][y]--, lim[x][y + ]--, lim[x + ][y + ]--;

     bool can_put = true;
     for (int i = ; i < ; i++) {
         int xx = x + dx[i], yy = y + dy[i];
         if (!ok(xx, yy)) { can_put = false; break; }
     }
     if (can_put) {
         int f1 = findn((x - )*n + y), f2 = findn(x*n + y + );
         if (f1 != f2) {
             ans[x][y] = ;
             int tmp = pre[f2];
             pre[f2] = f1;
             if (dfs(x, y + )) return true;
             pre[f2] = tmp;
         }
     }

     cur[x][y]--, cur[x + ][y + ]--;
     cur[x][y + ]++, cur[x + ][y]++;
     can_put = true;
     for (int i = ; i < ; i++) {
         int xx = x + dx[i], yy = y + dy[i];
         if (!ok(xx, yy)) { can_put = false; break; }
     }
     if (can_put) {
         int f1 = findn(x*n + y), f2 = findn((x - )*n + y + );
         if (f1 != f2) {
             ans[x][y] = -;
             int tmp = pre[f1];
             pre[f1] = f2;
             if (dfs(x, y + )) return true;
             pre[f1] = tmp;
         }
     }

     cur[x][y + ]--, cur[x + ][y]--;
     lim[x][y]++, lim[x + ][y]++, lim[x][y + ]++, lim[x + ][y + ]++;
     return false;
 }

 int main()
 {
     //freopen("input.txt", "r", stdin);
     int iCase;
     scanf("%d", &iCase);
     while (iCase--) {
         scanf("%d", &n);
         n++;
         char ss[maxn];
         for (int i = ; i <= n * n; i++) pre[i] = i;
         memset(cur, , sizeof(cur));

         for (int i = ; i <= n; i++) {
             scanf("%s", ss + );
             for (int j = ; j <= n; j++) {
                 if (ss[j] == '.') gra[i][j] = -;
                 else gra[i][j] = ss[j] - '';

                 lim[i][j] = ;

                 if ((i ==  || i == n) && (j ==  || j == n)) {
                     lim[i][j] = ;
                     continue;
                 }
                 if (i ==  || j ==  || i == n || j == n) {
                     lim[i][j] = ;
                 }
             }
         }

         dfs(, );

         for (int i = ; i < n; i++) {
             for (int j = ; j < n; j++) {
                 if (ans[i][j] == ) printf("\\");
                 else printf("/");
             }
             printf("\n");
         }
     }
     return ;
 }