Andrew NG 机器学习编程作业6 Octave

问题描述：使用SVM（支持向量机 ）实现一个垃圾邮件分类器。

在开始之前，先简单介绍一下SVM

①从逻辑回归的 cost function 到SVM 的 cost function

逻辑回归的假设函数如下：

h_θ(x)取值范围为[0,1]，约定h_θ(x)>=0.5，也即θ^T·x  >=0时，y=1；比如h_θ(x)=0.6，此时表示有60%的概率相信 y 等于1

显然，要想让y取值为1，h_θ(x)越大越好，因为h_θ(x)越大，y 取值为1的概率也就越大，也即：更好把握相信 y 等于1。而要想h_θ(x)越大，也就是θ^T·x远远大于0

The larger θ

^T

·x is, the larger also is h

_θ

(x) = p(y = 1|x; w, b), and thus also the higher our degree of “confidence”
that the label is 1

同理，y 等于0，也可以通过类似的推理得到：要想让 y 取值为0，则h_θ(x)越小越好，而要想h_θ(x)越小，也就是θ^T·x远远小于0

逻辑回归的代价函数(cost function)如下：(为了方便讨论，假设 training examples 只有一个，即：m = 1)

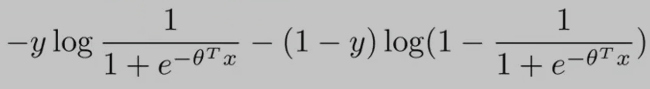
从上面的cost function公式 可以看出：当y==0时，只有右边的那部分式子起作用；当y==1时，(1-y==0)只有左边的那部分式子起作用。

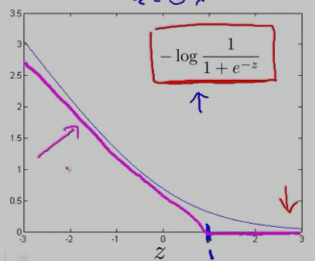
y==1时，逻辑回归的代价函数的图形表示如下：可以看出，逻辑回归的代价函数在整个坐标轴上是连续的。

在上面的y==1时的逻辑回归代价函数的基础上，构造一条新的代价函数曲线，记为cost₁(z) ,(用紫色的两条直线 线段表示，z==1处是转折点)，如下图：在z==1 点，新的代价函数是不连续的。

同理，y==0时，逻辑回归的代价函数的图形表示如下图：可以看出，逻辑回归的代价函数在整个坐标轴上是连续的。

在上面的y==0时的逻辑回归代价函数的基础上，构造一条新的代价函数曲线，记为cost₀(z)(用紫色的两条直线 线段表示，z== -1处是转折点)，如下图：在z== -1 点，新的代价函数是不连续的。

使用上面新构造的两条函数曲线：cost₀(z)  和 cost₁(z)  (z 等于θ^T·x)，组成了支持向量机(SVM)的cost function，如下：

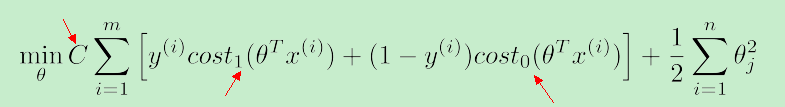
对于training example的数目 m 而言，它是一个常量，故在SVM的cost function中 去掉了 m

因此，总结一下，得到SVM的代价函数如下：

对于SVM而言，y==1时，要求：θ^T·x>=1；y==0时，要求：θ^T·x<=-1

可以看出：相比于逻辑回归，SVM中的 label of result y 等于 1 时，要求θ^T·x大于等于1，而不是0，这就相当于多了提高了限制条件，多了一层保障。

另外，SVM的代价函数中的 参数 C 就相当于逻辑回归中的lambda(λ)

因为，我们的目的是最小化 cost function，当 C 很大时，与 C 相乘的这一项只有非常接近于0时，才能让 cost function变小啊...当 C 非常大时，代价函数就等价于：min (1/2)·Σθ²_j

②SVM的decision boundary

相比于逻辑回归，SVM能实现更复杂的非线性分类问题。先讨论下线性可分的情况下如何选择更好的 decision boundary？

对于样本数据而言，可能有很多种不同的 decision boundary 来对样本进行划分，比如：下图中就有三条 decision boundary，但我们觉得，黑色的那条decision boundary更好地将样本数据分开。

黑色的那条 decision boundary 的优点是：有着更大的 margin。这就是SVM分类器的特点：总是尽可能地找出一条最大 margin 的decision boundary，因此SVM有时也称为 Large Margin Classifier。

对于下图中的数据(有一个红色的叉很“奇特”)，SVM又会怎样寻找 decision boundary呢？

当SVM的代价函数中的C不是太大的情况下，SVM还是会坚持黑色那条decision boundary，而不是转化成紫色的那条 decision boundary。

当SVM的代价函数中的参数C很大时，它就很可能会选择紫色的那条 decision boundary了。但是，在实际应用上，C 不会是 很大很大的，因此，尽管样本中出现了“奇异点”样本，SVM还是会坚持黑色那条decision boundary，从而具有一定的“容错性”

③SVM为什么是大间距分类器？(Why Large Margin?)

假设当C很大时，代价函数：min (1/2)·Σθ²_j 可以表示成向量的乘法形式：min (1/2)θ^T·θ

因为：Σθ_j² = (θ₁² +θ₂² +.... +θ_n²) = (θ₁，θ₂，....,θ_n)^T• (θ₁，θ₂，....,θ_n) = ||θ||²

因此，我们把代价函数 转化成了：向量θ的范数，如下图 (n=2)

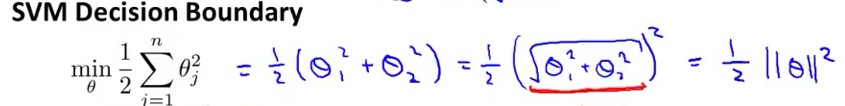
在最小化代价函数时，服从于下面条件：

θ

^T

·x

⁽ⁱ⁾

  >= 1    if  y==1
θ

^T

·x

⁽ⁱ⁾

 <= -1    if y==0

向量乘法与向量投影之间的关系：假设有两个向量a，向量b；向量a、b之间的夹角为theta，由向量乘法公式：a*b=||a||*||b||*cos(theta)。其实，||b||*cos(theta)就是向量b在向量a上的投影。

根据向量的投影，θ^T·x⁽ⁱ⁾ = p⁽ⁱ⁾•||θ||，其中p⁽ⁱ⁾是向量 x⁽ⁱ⁾ 在 向量θ 方向上的投影。θ^T·x⁽ⁱ⁾ = p⁽ⁱ⁾•||θ|| 的示意图如下：

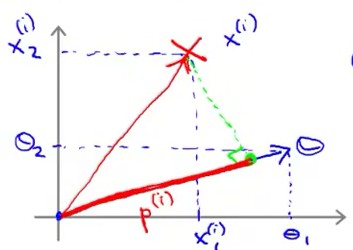
从而，将代价函数服从的条件转化成了“向量投影”表示，如下：

要想最小化代价函数(1/2)·Σθ²_j ，就得让||θ||尽可能地小；但是又得满足条件：θ^T·x⁽ⁱ⁾ >= 1 if y==1  and  θ^T·x⁽ⁱ⁾ <= -1 if y==0

根据：θ^T·x⁽ⁱ⁾ = p⁽ⁱ⁾•||θ||。因此，要想θ^T·x⁽ⁱ⁾ 尽可能地大于等于 1 ，就得让p⁽ⁱ⁾ 尽可能地大，这样p⁽ⁱ⁾•||θ|| 才有更大的可能 大于等于1。

（不能让||θ||尽可能地大，因为||θ||大了，代价函数就大了，而我们的目标是最小化代价函数）

好，既然现在的目标是让p⁽ⁱ⁾尽可能地大，那p⁽ⁱ⁾代表的意义是什么呢？就是：margins（间距），这也是SVM被称为 大间距分类器 的原因。
那 p⁽ⁱ⁾ 为什么代表的是间距呢？看下图：

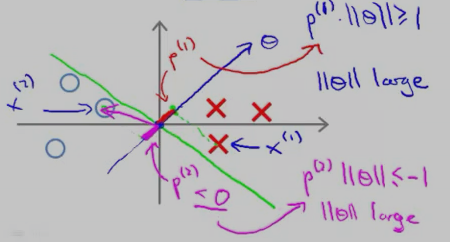
红色的叉叉 和 圆圈 表示的是训练的样本，我们用一条绿色的线(decision boundary)将叉叉 和 圆圈 分开。向量θ 的方向是与decision boundary 垂直的。

对于“红色的叉叉”这个样本x⁽¹⁾而言，它的几何间距是 p⁽¹⁾；对于圆圈样本 x⁽²⁾ 而言，它的几何间距是p⁽²⁾

从上图中可以看出，p⁽¹⁾ 和p⁽²⁾ 的长度 都比较短，因此，要想让p⁽ⁱ⁾•||θ|| 大于等于1 或者 小于等于-1，只能让||θ||大一点了，而||θ||要是很大，代价函数就大了，而最小化SVM的代价函数的意义就是：找出一组参数(θ₁，θ₂......θ_n)，使得代价函数尽可能地小。因此，SVM是不会选择 p⁽¹⁾ 长度 小的 decision boundary的。

再来看一个投影长度p⁽ⁱ⁾ 比较长的例子：

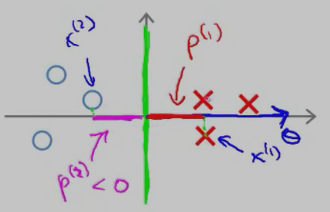
红色的叉叉 和 圆圈 表示的是训练的样本，我们用一条绿色的线(decision boundary)将叉叉 和 圆圈 分开，此时的decision boundary刚好是 y 轴(竖直线)；红色的叉叉样本x⁽¹⁾ 在向量上的投影p^{(1 )}刚好是x⁽¹⁾ 的 x 轴的坐标，它要比斜着的绿色decision boundary 上的投影 要长。

因此，SVM 会选择这条竖直的绿色 decision boundary 作为分类边界。它的 Margin 的示意图如下：

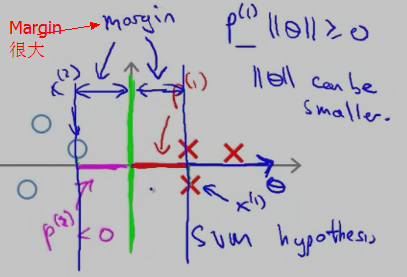
在上面的描述中，我们是先假设 SVM 的cost function 中的参数 C 很大，只留下了 θ（min (1/2)·Σθ²_j ）。然后根据 样本x⁽ⁱ⁾ 在 θ向量上 的投影尽可能大 使得Margin很大，从而选择Margin大的 decision boundary，下面将从另一个角度来讨论为什么选择大的 margins（参考 cs229-notes3.pdf）

首先看下图中的一个线性可分的例子：

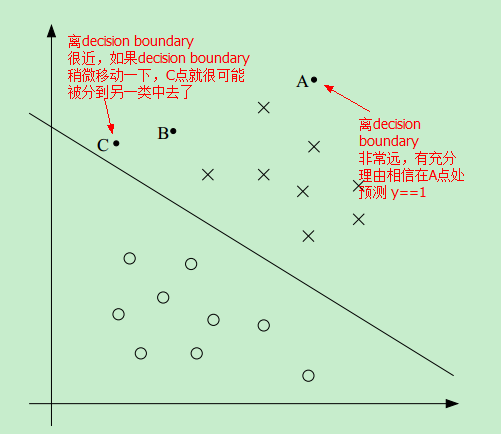
因此，如果我们能找到这样一条 decision boundary，让所有的点尽可能地离该decision boundary 远，这样我们就更有理由预测 y==1 或者 y==0

比如，相比于C点，我们更有理由相信 A点属于 positive 这一类，即更相信 预测 A点的 y==1 而不是预测C点的 y==1