基于Manhattan最小生成树的莫队算法

点u，v的Manhattan距离：distance（u，v）= |x2-x1|+|y2-y1|

Manhattan最小生成树：边权值为两个点Manhattan距离的最小生成树。

普通算法：prim复杂度O(N²)，或者处理出所有边，那么kruskal复杂度O(N²logN)，这么庞大的复杂度显然是不行的

Manhattan最小生成树算法：以一个点为原点建立直角坐标系，在每45度内只会向距离该点最近的一个点连边。

简略证明：

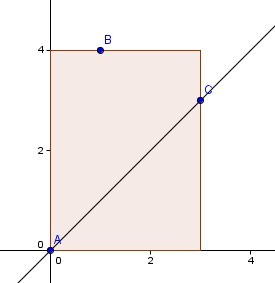
　　如图，我们不妨设|AB|<=|AC|;

　　那么可以证明|AC|>=|BC|，证明如下

　　　　

　　　　　　|AB|=x1+y1，|AC|=x2+y2，|BC|=|x1-x2|+|y1-y2|。而由于B和C都在y轴向右45度的区域内，有y-x>0且x>0。

　　　　　　下面我们分情况讨论：

1. 1. 1. 1. x1>x2且y1>y2。这与|AB|≤|AC|矛盾；
         2. x1≤x2且y1>y2。此时|BC|=x2-x1+y1-y2，|AC|-|BC|=x2+y2-x2+x1-y1+y2=x1-y1+2*y2。由前面各种关系可得y1>y2>x2>x1。假设|AC|<|BC|即y1>2*y2+x1，那　　么|AB|=x1+y1>2*x1+2*y2，|AC|=x2+y2<2*y2<|AB|与前提矛盾，故|AC|≥|BC|；
         3. x1>x2且y1≤y2。与2同理；
         4. x1≤x2且y1≤y2。此时显然有|AB|+|BC|=|AC|，即有|AC|>|BC|。

　　　　　　综上有|AC|≥|BC|，也即在这个区域内只需选择距离A最近的点向A连边。　　

　　显然|AC|是权值最大的边，那么我们在建立最小生成树时必然不会选择它，即我们必然连接点A,B而不是A,C

接下去用kruskal算法在O(NlogN)复杂度内处理这N条边：

　　

我们只需考虑在一块区域内的点，其他区域内的点可以通过坐标变换“移动”到这个区域内。为了方便处理，我们考虑在y轴向右45度的区域。在某个点A(x0,y0)的这个区域内的点B(x1,y1)满足x1≥x0且y1-x1>y0-x0。这里对于边界我们只取一边，但是操作中两边都取也无所谓。那么|AB|=y1-y0+x1-x0=(x1+y1)-(x0+y0)。在A的区域内距离A最近的点也即满足条件的点中x+y最小的点。因此我们可以将所有点按x坐标排序，再按y-x离散，用线段树或者树状数组维护大于当前点的y-x的最小的x+y对应的点。时间复杂度O(NlogN)。

至于坐标变换，一个比较好处理的方法是第一次直接做；第二次沿直线y=x翻转，即交换x和y坐标；第三次沿直线x=0翻转，即将x坐标取相反数；第四次再沿直线y=x翻转。注意只需要做4次，因为边是双向的。

至此，整个问题就可以在O(NlogN)的复杂度内解决了。

举例：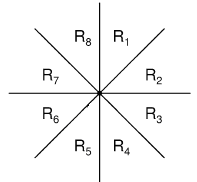

　

显然，边(i,j), (j,k), (i,k)构成一个环<i,j,k>，而(i,k)一定是最长边，可以被删去。所以我们只连边(i,j)。

为了避免重复加边，我们只考虑R1~R4这4个区域。（总共加了4N条边）

这4个区域的点(x,y)要满足什么条件？

• 如果点(x,y)在R1，它要满足：x ≥ xi ,y – x ≥ yi – xi（最近点的x + y最小）
• 如果点(x,y)在R2，它要满足：y ≥ yi ,y – x ≤ yi – xi（最近点的x + y最小）
• 如果点(x,y)在R3，它要满足：y ≤ yi ,y + x ≥ yi + xi（最近点的y – x最小）
• 如果点(x,y)在R4，它要满足：x  ≥ xi ,y + x ≤ yi – xi（最近点的y – x最小）

基于Manhattan算法的莫队算法：

对于询问[l,r],我们可以将其看做一个二维平面上的点，如果询问从状态[l,r]转移到询问[l,r+1]所需时间为O(1)，那么就可以用莫队算法解决。

显然询问[l1,r1]转移到询问[l2,r2]所需的时间为|l2-l1|+|r2-r1|,这时候我们可以发现这个需要的时间是两个点的Manhattan距离，

那么我们就可以用Manhattan最小生成树来优化这些所有询问之间状态转移所需的时间。

　　

我们先对序列分块，然后以询问左端点所在的分块的序号为第一关键字，右端点的大小为第二关键字进行排序，按照排序好的顺序计算，复杂度就会大大降低。

• 分块相同时，右端点递增是的，分块共有个，复杂度为
• 分块转移时，右端点最多变化，分块共有个，复杂度为
• 分块相同时，左端点最多变化，分块转移时，左端点最多变化，共有个询问，复杂度为

模板题：bzoj：小z的袜子

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define MAXN 50005
#define ll long long
using namespace std;
struct Query{
    int L,R,id;
}q[MAXN];//所有询问
int s,col[MAXN];//col[i]是第i个袜子的颜色
ll ans[MAXN][],cnt[MAXN];//cnt[i]表示当前区间里颜色i出现的次数
/*先以块为关键字从小到大排序，
再以右端点为关键字进行从小到大排序*/
bool cmp(Query a,Query b){
    if(a.L/s==b.L/s) return a.R<b.R;
    return a.L/s<b.L/s;
}
//求最大公约数
int gcd(ll a,ll b){
    return a?gcd(b%a,a):b;
}
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    s=(int)sqrt(n);
    for(int i=;i<=n;i++)
        scanf("%d",&col[i]);
    for(int i=;i<m;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        q[i]=(Query){a,b,i};
    }
    sort(q,q+m,cmp);//把询问排序
    int L=,R=;
    ll res=;
    for(int i=;i<m;i++){//遍历每个询问
        while(R<q[i].R){//右边界还没拓展到q[i].R，要往右边拓展
            R++;
            res+=(cnt[col[R]]+)*(cnt[col[R]]+)-cnt[col[R]]*cnt[col[R]];
            cnt[col[R]]++;
        }
        while(L<q[i].L){//左边界超过了q[i].L,要往右边回缩
            res-=cnt[col[L]]*cnt[col[L]]-(cnt[col[L]]-)*(cnt[col[L]]-);
            cnt[col[L]]--;
            L++;
        }
        while(R>q[i].R){//右边界超过了q[i].R,要往左边回缩
            res-=cnt[col[R]]*cnt[col[R]]-(cnt[col[R]]-)*(cnt[col[R]]-);
            cnt[col[R]]--;
            R--;
        }
        while(L>q[i].L){//左边界还没拓展到q[i].L,要往左边拓展
            L--;
            res+=(cnt[col[L]]+)*(cnt[col[L]]+)-cnt[col[L]]*cnt[col[L]];
            cnt[col[L]]++;
        }
        ans[q[i].id][]=res-R+L-;//分子
        ans[q[i].id][]=(ll)(R-L+)*(R-L);//分母
    }

    for(int i=;i<m;i++){
        int G=gcd(ans[i][],ans[i][]);
        ans[i][]/=G;
        ans[i][]/=G;
        if(!ans[i][])//如果分子是0(可能出现的)
            ans[i][]=;
    }
    for(int i=;i<m;i++)
        printf("%lld/%lld\n",ans[i][],ans[i][]);
    return ;
}