GC算法

标记-清除算法
复制算法
标记-整理算法
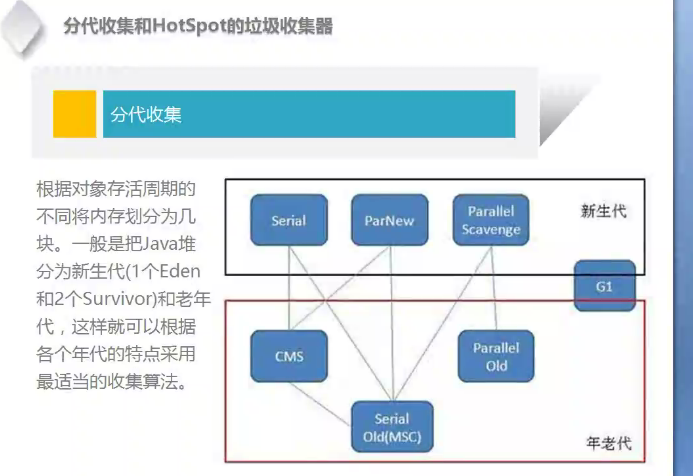
分代收集 新生代--[15次GC]-->老年代
新生代：复制算法
老年代: 标记-清除算法或标记-整理算法

GC策略采用的何种算法
引用计数算法
根搜索算法

内存泄漏和内存溢出的区别
jvm 无法gc的内存 造成内存泄漏 举例：数组

stopWorld[Full GC]

jvm调优：
减少GC的时间和频率，尤其减少Full GC的次数

参数配置：

虚拟机栈和本地方法栈溢出： -Xss256k

Java堆溢出：-Xms5M -Xmx5M -XX:+PrintGCDetails -verbose:gc

方法区和运行时常量池溢出：-XX:MaxMetaspaceSize=3M

本机直接内存溢出：-Xmx10M -XX:MaxDirectMemorySize=10M

JVM 虚拟机笔记的更多相关文章

  1. jvm虚拟机笔记<三> 类文件结构与类加载机制

    java虚拟机具有语言无关系,它只和“class文件“这种特定的二进制文件格式绑定. 不同语言的编译器将对应的程序编译成字节码文件(*.class),送给jvm执行. class文件本质上就是一张表, ...

  2. jvm虚拟机笔记<五> 编译期优化

    JVM的编译器可以分为三个编译器: 1.前端编译器:把.java转变为.class的过程.如Sun的Javac.Eclipse JDT中的增量式编译器(ECJ). 2.JIT编译器:把字节码转变为机器 ...

  3. jvm虚拟机笔记<六> 运行期优化

    这节我们总结一下JVM运行期的优化问题. https://www.cnblogs.com/zhouyuqin/p/5224573.html JVM运行期优化 即时编译器(JIT) 编译对象与触发条件 ...

  4. jvm虚拟机笔记<四> 虚拟机字节码执行引擎

    一.运行时栈帧结构 栈帧是用于支持虚拟机进行方法调用和执行的数据结构,是虚拟机栈的栈元素. 栈帧存储了局部变量表,操作数栈,动态连接,和返回地址等. 每一个方法的执行 对应的一个栈帧在虚拟机里面从入栈 ...

  5. jvm虚拟机笔记<二> 垃圾回收与内存分配

    确定对象已废弃需要两步: 利用可达性分析算法(与GC roots有关联——虚拟机栈中的对象,方法区静态对象,方法区常量对象,本地方法引用的对象)判断是否需要回收. 是否覆盖过finalize方法并执行 ...

  6. jvm虚拟机笔记<一> 内存区域

    运行时数据区域: 程序计数器:字节码的行号指示器. 虚拟机栈:为每个方法创建一个栈帧(存放方法中的局部变量,变量引用等). 本地方法栈:存放本地方法. ------------------------ ...

  7. JVM学习笔记：虚拟机的类加载机制

    JVM类加载机制分两部分来总结: (1)类加载过程 (2)类加载器 一.JVM类加载过程 类的加载过程:加载 →连接(验证 → 准备 → 解析)→ 初始化. 类的生命周期:加载 →连接(验证 → 准备 ...

  8. Java虚拟机笔记（五）：JVM中对象的分代

    为什么要分代 为什么需要把堆分代?不分代不能完成他所做的事情么?其实不分代完全可以,分代的唯一理由就是优化GC性能.你先想想,如果没有分代,那我们所有的对象都在一块,GC的时候我们要找到哪些对象没用, ...

  9. 【Java虚拟机】JVM学习笔记之GC

    JVM学习笔记二之GC GC即垃圾回收,在C++中垃圾回收由程序员自己来做,例如可以用free和delete来回收对象.而在Java中,JVM替程序员来执行垃圾回收的工作,下面看看GC的详细原理和执行 ...

随机推荐

  1. Docker镜像的使用

    当运行容器时,使用的镜像如果在本地中不存在,docker 就会自动从 docker 镜像仓库中下载,默认是从 Docker Hub 公共镜像源下载. 下面我们来学习: 1.管理和使用本地 Docker ...

  2. 【BZOJ1211】【HNOI2004】树的计数 prufer序列

    题目描述 给你\(n\)和\(n\)个点的度数,问你有多少个满足度数要求的生成树. 无解输出\(0\).保证答案不超过\({10}^{17}\). \(n\leq 150\) 题解 考虑prufer序 ...

  3. 反射中Class.forName()和classLoader的区别

    搞清楚两者之间区别前,我们来了解下类加载过程. 一.类加载过程 1.加载 通过一个类的全限定名来获取定义此类的二进制字节流. 将这个字节流所代表的静态存储结构转化为方法区的运行时数据结构. 在内存中生 ...

  4. Android 性能优化提示

    原文 http://developer.android.com/guide/practices/design/performance.html 性能优化 Android应用程序运行的移动设备受限于其运 ...

  5. 【BZOJ3165】[HEOI2013]Segment（李超线段树）

    [BZOJ3165][HEOI2013]Segment(李超线段树) 题面 BZOJ 洛谷 题解 似乎还是模板题QwQ #include<iostream> #include<cst ...

  6. js 时间类函数

    js 时间类是  Date() var currtime = new Date();// 实例一个时间,是当前时间 接收一个时间戳为参数 var time2=new Date(currtime.get ...

  7. python服务器文件上传下载+GUI【tkinter】

    大概就是一个通过应用程序来和服务器打交道的这么一个,小东西 1.GUI 用的是tkinter # -*- coding: UTF-8 -*- from tkinter import * import ...

  8. django 模板语言

    母版与继承: <!DOCTYPE html> <html lang="en"> <head> <meta charset="UT ...

  9. Pycharm For Linux

    之前说过JetBrains系列的破解方式:https://www.cnblogs.com/dunitian/p/8478252.html 现在说下怎么固定到任务栏,速度版 详细讲解可以看之前说安装微信 ...

  10. hdu 4283"You Are the One"(区间DP)

    传送门 https://www.cnblogs.com/violet-acmer/p/9852294.html 题意: 有n个屌丝排成一排,每个屌丝都有一个不开心值a[ i ]( i=1,2,3,.. ...