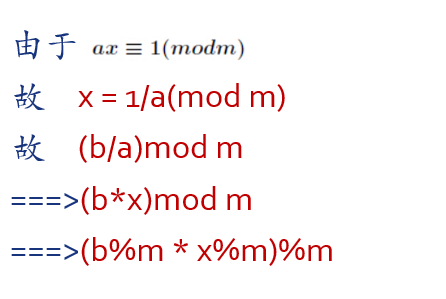牛客Wannafly挑战赛13-BJxc军训-费马小定理、分式取模、快速幂
参考:https://blog.csdn.net/qq_40513946/article/details/79839320
传送门:https://www.nowcoder.com/acm/contest/80/B
题意:输入n,m,求 (n*n-m)/n*n 在 取模998244353下的解;
思路:
ac代码:
#include <iostream>
using namespace std; typedef long long ll;
const int md = ;
ll fpow(ll a,ll n)//快速幂
{
ll res = ;
while(n)
{
if(n&)
res = res*a%md;
a = a*a%md;
n>>=;
}
return res;
}
int main(){
int n,m;
cin>>n>>m;
ll t = n*n-m;
ll ans = t%md*(fpow( n*n , md-)%md)%md;
cout<<ans<<endl; return ;
}
牛客Wannafly挑战赛13-BJxc军训-费马小定理、分式取模、快速幂的更多相关文章
- HDU4675【GCD of scequence】【组合数学、费马小定理、取模】
看题解一开始还有地方不理解,果然是我的组合数学思维比较差 然后理解了之后自己敲了一个果断TLE.... 我以后果然还得多练啊 好巧妙的思路啊 知识1: 对于除法取模还需要用到费马小定理: a ^ (p ...
- HDU4704Sum 费马小定理+大数取模
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=4704 题目大意: 看似复杂,其实就是求整数n的划分数,4=1+1+2和4=1+2+1是不同的.因而可 ...
- hdu 4704 Sum【组合数学/费马小定理/大数取模】By cellur925
首先,我们珂以抽象出S函数的模型:把n拆成k个正整数,有多少种方案? 答案是C(n-1,k-1). 然后发现我们要求的是一段连续的函数值,仔细思考,并根据组合数的性质,我们珂以发现实际上答案就是在让求 ...
- HDU 4549 (费马小定理+矩阵快速幂+二分快速幂)
M斐波那契数列 Time Limit: 1000MS Memory Limit: 32768KB 64bit IO Format: %I64d & %I64u Submit Statu ...
- [ACM] hdu 3923 Invoker (Poyla计数,高速幂运算,扩展欧几里得或费马小定理)
Invoker Problem Description On of Vance's favourite hero is Invoker, Kael. As many people knows Kael ...
- 牛客wannafly 挑战赛14 B 前缀查询(trie树上dfs序+线段树)
牛客wannafly 挑战赛14 B 前缀查询(trie树上dfs序+线段树) 链接:https://ac.nowcoder.com/acm/problem/15706 现在需要您来帮忙维护这个名册, ...
- 牛客训练四:Applese 涂颜色(费马小定理+快速幂)
题目链接:传送门 思路: 考虑每一列有2种颜色,总共有n行,每一行的第一个格确定颜色,由于左右颜色不相同,后面的行就确定了. 所以总共有2^n中结果. 由于n太大,所以要用到费马小定理a^n%mod= ...
- UVA10200-Prime Time/HDU2161-Primes,例题讲解,牛逼的费马小定理和欧拉函数判素数。
10200 - Prime Time 此题极坑(本菜太弱),鉴定完毕,9遍过. 题意:很简单的求一个区间 ...
- Newcoder Wannafly13 B Jxy军训(费马小定理、分数在模意义下的值)
链接:https://www.nowcoder.com/acm/contest/80/B 题目描述 在文某路学车中学高一新生军训中,Jxc正站在太阳下站着军姿,对于这样的酷热的阳光,Jxc 表示非常不 ...
随机推荐
- 移动端开发用touch事件还是click事件
前端开发现在包含了跨浏览器,跨平台(不同操作系统)和跨设备(不同尺寸的设备)开发. 在移动开发的过程中,到底选取touch事件还是click事件?对了,请不要鄙视click,click在移动端开发用着 ...
- Web Worker 多线程
Web Workers多线程 1 浏览器把所有事件都通过操作系统安排到事件队列中(例如:你去一个·窗口买菜,需要排队):浏览器使用单线程处理队列中的事件和执行用户代码(也就是单线程:web work ...
- html以前没有学到的标签
<q>标签,短文本引用 <blockquote>标签,长文本引用 <address>标签,为网页加入地址信息 <code>标签,插入单行代码 <p ...
- abc -- 牛客
题目描述 设a.b.c均是0到9之间的数字,abc.bcc是两个三位数,且有:abc+bcc=532.求满足条件的所有a.b.c的值. 输入描述: 题目没有任何输入. 输出描述: 请输出所有满足题目条 ...
- ccf 201903-5 317号子任务(60分)
看到这题,第一印象,用dijkstra算法求n次单源最短路,时间复杂度O(n^3),超时30分妥妥的. 于是用优先队列优化,O(n*mlogm),快很多,但依然30. 那么不妨换一种思路,题目要求的是 ...
- 手写Struts,带你深入源码中心解析
个人剖析,不喜勿喷 扫码关注公众号,不定期更新干活 在此申明本博文并非原创,原文:http://blog.csdn.net/lenotang/article/details/3336623,本文章是在 ...
- ES 27 - Elasticsearch脚本的使用实践
目录 1 关于脚本 2 脚本使用的最佳实践 2.1 创建脚本并存储 2.2 脚本的缓存 2.3 Script Field - 脚本字段 本文以 ES 6.6.0 版本为例进行演示. 1 关于脚本 ES ...
- 【干货】基于镜像部署的Gitlab-CI/CD实践和坑位指南
引言 看过前文的博友可能注意到我是把 部署dll文件拷贝到生产机器,之后在生产机器上使用docker-compose即时创建镜像, 并没有完成CI/CD, 只是在原来传统部署方式下 将部署文件容器化. ...
- java之异常详解
一.什么是异常? 异常就是有异于常态,和正常情况不一样,有错误出错.在java中,阻止当前方法或作用域正常运行的情况,称之为异常. 二.异常体系 Java把异常当作对象来处理,并定义一个基类java. ...
- zabbix自发现item监控
在zabbix监控中,我们可以通过自带item的可以和自定义key进行监控,但是当所需要的监控项不确定,比如key会根据时间进行变化时,这时候我们就不能把item的key定义死,要通过自发现这个高级功 ...