索引的底层实现(B 树)
一、B 树
1、B-Tree介绍
B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;
定义
B-Tree是一种多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
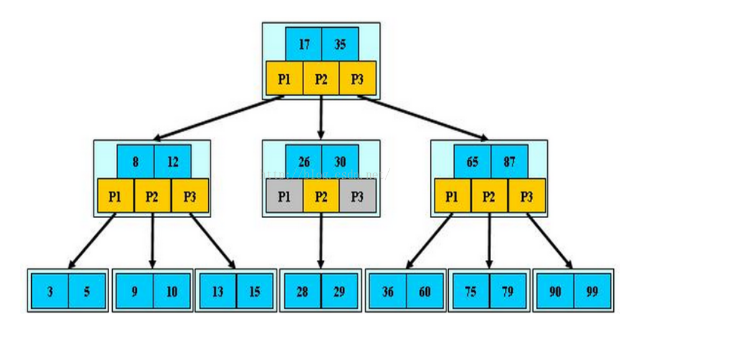
特性
B-树的特性:
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
2、B+Tree介绍
定义
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
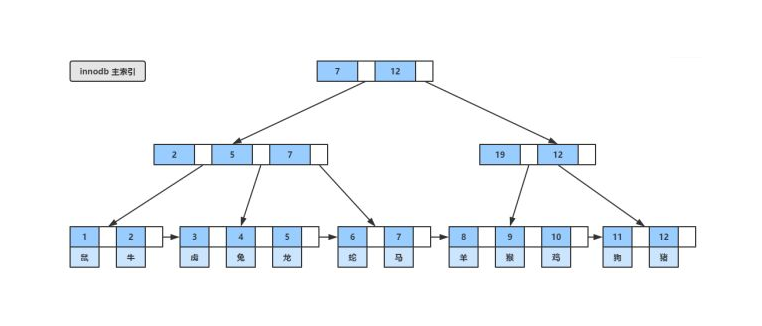
特性
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4.更适合文件索引系统;
3、B树与B+树区别
这都是由于B+树和B具有这不同的存储结构所造成的区别,以一个m阶树为例。
关键字的数量不同;B+树中分支结点有m个关键字,其叶子结点也有m个,其关键字只是起到了一个索引的作用,但是B树虽然也有m个子结点,但是其只拥有m-1个关键字。
存储的位置不同;B+树中的数据都存储在叶子结点上,也就是其所有叶子结点的数据组合起来就是完整的数据,但是B树的数据存储在每一个结点中,并不仅仅存储在叶子结点上。
分支结点的构造不同;B+树的分支结点仅仅存储着关键字信息和儿子的指针(这里的指针指的是磁盘块的偏移量),也就是说内部结点仅仅包含着索引信息。
查询不同;B树在找到具体的数值以后,则结束,而B+树则需要通过索引找到叶子结点中的数据才结束,也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径
二、索引底层实现
1、MyISAM 索引实现
MyISAM 引擎使用 B+Tree 作为索引结构,叶节点的 data 域存放的是数据记录
的地址。
主索引与辅助索引的区别(对某列建立索引):
在结构上没有任何区别,只是主索引要求 key 是唯一的,而辅助索引的 key 可以重复
主索引(聚集索引)也就是表的主键,是建表时指定的,并且是唯一的
辅助索引(非聚集索引)是对表有其他需要可以添加创建的
下图是 MyISAM 索引的原理图: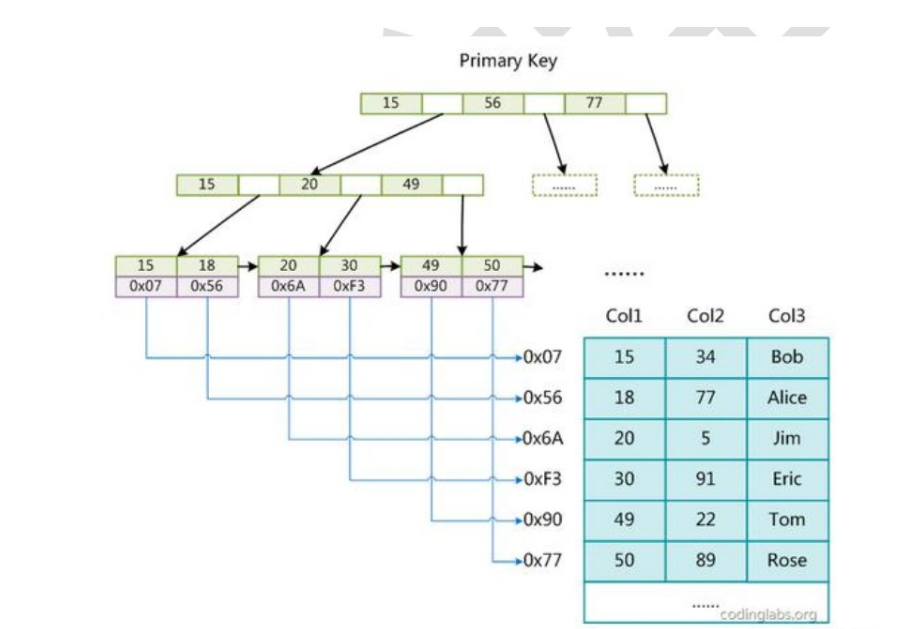
索引过程:
MyISAM 中索引检索的算法为首先按照 B+Tree 搜索算法搜索索引,如果指定的 Key 存在,则取出其data 域的值,然后以 data 域的值为地址,读取相应数据记录。
2、 InnoDB索引实现
1、InnoDB 的数据文件本身就是索引文件。从上文知道,MyISAM 索引文件和数据文件是分离的,索引文件仅保存数据记录的地址。
而在InnoDB 中,表数据文件本身就是按 B+Tree 组织的一个索引结构,这棵树的叶点data 域保存了完整的数据记录。这个索引的 key 是数据表的主键,因此 InnoDB 表数据文件本身就是主索引。
InnoDB 要求表必须有主键(MyISAM 可以没有),如果没有显式指定,则 MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键,如果不存在这种列,则MySQL 自动为 InnoDB 表生成一个隐含字段作为主键,类型为长整形
2、第二个与 MyISAM 索引的不同是 InnoDB 的辅助索引 data 域存储相应记录主键的值而不是地址。换句话说,InnoDB 的所有辅助索引都引用主键作为 data 域。
辅助索引搜索需要检索两遍索引:首先检索辅助索引获得主键,然后用主键到主索引中检索获得记录。
3、主键过长导致:
因为所有辅助索引都引用主索引,过长的主索引会令辅助索引变得过大。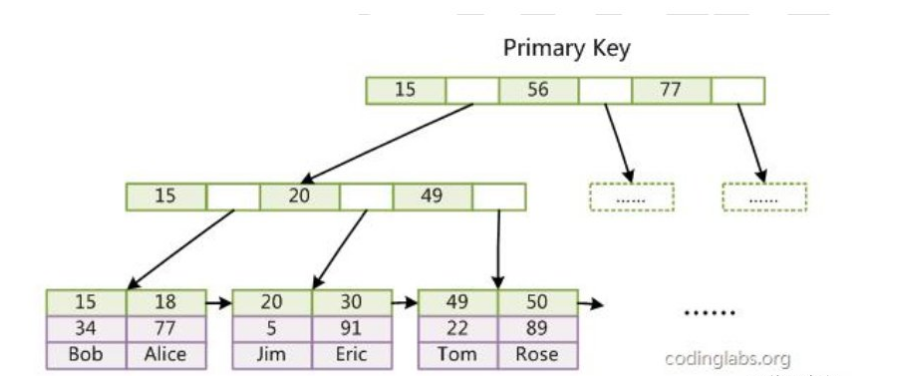
索引的底层实现(B 树)的更多相关文章
- 不懂数据库索引的底层原理?那是因为你心里没点b树
本文在个人技术博客不同步发布,详情可用力戳 亦可扫描屏幕右侧二维码关注个人公众号,公众号内有个人联系方式,等你来撩... 前几天下班回到家后正在处理一个白天没解决的bug,厕所突然传来对象的声音: ...
- (转)数据库_不懂数据库索引的底层原理?那是因为你心里没点BTree
原文地址:https://www.cnblogs.com/sujing/p/11110292.html 要了解数据库索引的底层原理,我们就得先了解一种叫树的数据结构,而树中很经典的一种数据结构就是二叉 ...
- MySQL索引(二)B+树在磁盘中的存储
MySQL索引(二)B+树在磁盘中的存储 回顾  上一篇文章<MySQL索引为什么要用B+树>讲了MySQL为什么选择用B+树来作为底层存储结构,提了两个知识点: B+树索引并不能直接找 ...
- mysql系列十、mysql索引结构的实现B+树/B-树原理
一.MySQL索引原理 1.索引背景 生活中随处可见索引的例子,如火车站的车次表.图书的目录等.它们的原理都是一样的,通过不断的缩小想要获得数据的范围来筛选出最终想要的结果,同时把随机的事件变成顺序的 ...
- MongoDB索引存储BTree与LSM树(转载)
1.为什么 MongoDB 使用B-树,而不是B+树 MongoDB 是一种 nosql,也存储在磁盘上,被设计用在数据模型简单,性能要求高的场合.性能要求高,我们看B-树与B+树的区别: B+树内节 ...
- MySQL数据库索引的底层原理(二叉树、平衡二叉树、B-Tree、B+Tree)
1.MySQL数据库索引的底层原理 https://mp.weixin.qq.com/s/zA9KvCkkte2mTWTcDv7hUg
- MySQL索引的原理,B+树、聚集索引和二级索引
MySQL索引的原理,B+树.聚集索引和二级索引的结构分析 一.索引类型 1.1 B树 1.2 B+树 1.3 哈希索引 1.4 聚集索引(clusterd index) 1.5 二级索引(secon ...
- MySQL索引机制详解(B+树)
一.索引是什么? 索引是为了加速对表中数据行的检索而创建的一种分散存储的数据结构. 二.为什么要使用索引? 索引能极大的减少存储引擎需要扫描的数据量. 索引可以把随机IO变成顺序IO. 索引可以帮助我 ...
- 面对key数量多和区间查询低效问题:Hash索引趴窝,LSM树申请出场
摘要:Hash索引有两个明显的限制:(1)当key的数量很多时,维护Hash索引会给内存带来很大的压力:(2)区间查询很低效.如何对这两个限制进行优化呢?这就轮到本文介绍的主角,LSM树,出场了. 我 ...
随机推荐
- 【Redis】SpringBoot整合Redis
一.Maven依赖 <dependency> <groupId>org.springframework.boot</groupId> <artifactId& ...
- 3、pytest中文文档--编写断言
目录 编写断言 使用assert编写断言 编写触发期望异常的断言 特殊数据结构比较时的优化 为失败断言添加自定义的说明 关于断言自省的细节 复写缓存文件 去使能断言自省 编写断言 使用assert编写 ...
- java多线程之Executor 与 ExecutorService两个基本接口
一.Executor 接口简介 Executor接口是Executor框架的一个最基本的接口,Executor框架的大部分类都直接或间接地实现了此接口. 只有一个方法 void execute(Run ...
- length属性、length()方法和size()的方法的区别
JAVA 1. length属性是针对Java中的数组来说的,要求数组的长度可以用其length属性: 2.length()方法是针对字符串来说的,要求一个字符串的长度就要用到它的length()方法 ...
- VUE Node模式下,如何改变菜单的颜色,如何将超长文字缩略显示,在鼠标进入后展开全部显示,鼠标移出则恢复缩略显示
VUE Node模式下,如何改变菜单的颜色,如何将超长文字缩略显示,在鼠标进入后展开全部显示,鼠标移出则恢复缩略显示: “事件”引起变量值的变化,系统引擎自动根据变量值的变化刷新页面 在VUE Nod ...
- 洛谷 P1091合唱队列
吾王剑之所指,吾等心之所向 ——<Fate/stay night> 题目:https://www.luogu.org/problem/P ...
- PythonI/O进阶学习笔记_4.自定义序列类(序列基类继承关系/可切片对象/推导式)
前言: 本文代码基于python3 Content: 1.python中的序列类分类 2. python序列中abc基类继承关系 3. 由list的extend等方法来看序列类的一些特定方法 4. l ...
- Android四大组件初识之Service
Service作为Android四大组件之一,可以与Activity建立双向连接(绑定模式),提供数据和功能.也能够接收Intent单方面请求(调用模式),进行数据处理和调度功能. Service与A ...
- android 百度地图入门01 (史上最详没有之一)
最近一直和百度地图打交道,写几篇博客记录一下吧,目前最新版是4.0的 ,之前我用的是3.7的, 就以4.0的为例说一下最基本的配置流程吧. 一.准备工作 1.申请一个百度地图开发者账户--地址:htt ...
- Python网络爬虫实战(三)照片定位与B站弹幕
之前两篇已经说完了如何爬取网页以及如何解析其中的数据,那么今天我们就可以开始第一次实战了. 这篇实战包含两个内容. * 利用爬虫调用Api来解析照片的拍摄位置 * 利用爬虫爬取Bilibili视频中的 ...
