Dilated Convolutions 空洞卷积

Dilated Convolutions，中文一般称为空洞卷积或者扩张卷积，是一种改进的图像卷积方法。

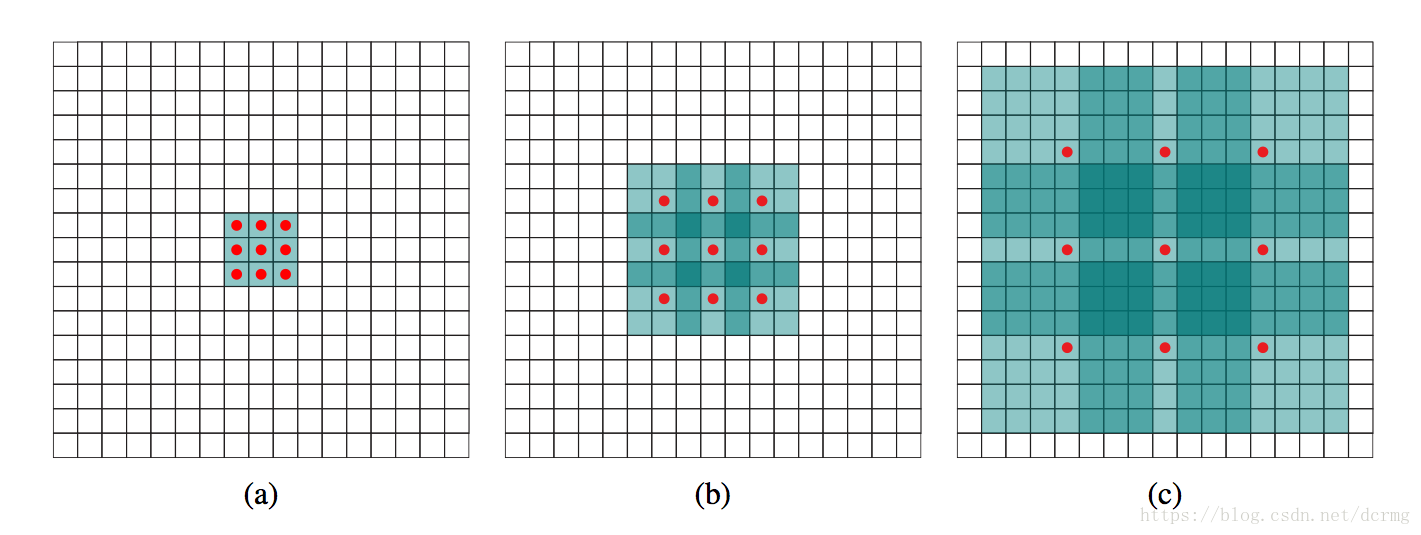
扩张卷积工作示意图如下：

图a是普通的卷积，感受野是3*3，相当于扩充dilation=0

图b是扩张卷积，感受野是7*7，dilation=2

图c是扩张卷积，感受野是15*15，dilation=4

 
扩张卷积中多了一个扩充率参数（dilation rate），用来控制扩张（空洞填充）的大小，扩充率参数越大，同等卷积核大小对应的感受野越大。扩充卷积对普通卷积的改进就是为了获得更大的感受野。

 

标准卷积在特定场景如图像语义分割下存在一定的问题，比如通过池化操作降低计算量，同时增大感受野，再通过反卷积（上采样）扩充图像到原始大小，这中间会丢失很多信息，特别是空间结构信息，另一个问题是小的物体信息无法复原重建出来。而在空洞卷积中，避免了使用池化操作的同时增大了感受野，不需要图像分辨率的压缩，保留了图像内部的数据结构，可以有比标准卷积更好的分割效果。