hdu 4753 Fishhead’s Little Game

状态压缩dp解博弈问题（记忆化搜索）。比赛的时候最后才开始做这道题，而且当时不知道为什么一直犯一些很2B的问题，导致没能ac，晚上看了看原先的代码，改了一下就MLE了。。。我原先是开的dp[1 << 24] 的记忆化数组，果断超内存了，然后仔细看了一下题目，发现题目中的n >= 12，也就是说用到的状态不超过2^12个，于是把满足情况的状态hash到2^12以内的数组就可以了。

思路：

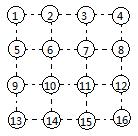
因为只有24条边，所以可以考虑把边压缩，于是就转化成了普通的状态了，然后用dp数组表示该状态下先手能得到的最大分值。也就是处于该状态时，先手放一条边以后得使得后手得分最少，因为总分是一定的，这样的话先手就可以得到最优解了。然后就记忆化搜索一下就可以了。我hash用的是数组存储，二分查找下标的方法，时间效率不是很高。。。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<fstream>
#include<sstream>
#include<bitset>
#include<vector>
#include<string>
#include<cstdio>
#include<cmath>
#include<stack>
#include<queue>
#include<stack>
#include<map>
#include<set>
#define FF(i, a, b) for(int i=a; i<b; i++)
#define FD(i, a, b) for(int i=a; i>=b; i--)
#define REP(i, n) for(int i=0; i<n; i++)
#define CLR(a, b) memset(a, b, sizeof(a))
#define debug puts("**debug**")
#define LL long long
#define PB push_back
using namespace std;

const int N= 1 << 13;
const int INF = 1e9;

int dp[N], n, mp[N];
int gogo[22][22], num;

void get_gogo()
{
    int i , j = 0;
    for(i = 1; i < 16; i ++)
    {
        if(i % 4 == 0) continue;
        gogo[i][i + 1] = j;
        j ++;
    }
    for(i = 1; i <= 12; i ++)
    {
        gogo[i][i + 4] = j;
        j ++;
    }
}

bool ok(int k, int i)
{
    return (k & (1 << i)) && (k & (1 << (i + 3))) && (k & (1 << ((i / 3) + i + 12))) && (k & (1 << ((i / 3) + i + 13)));
}

int get_f(int k)
{
    int i, j, ret = 0;
    for(i = 0; i < 9; i ++)
    {
        if((k & (1 << i)) && ok(k, i))
            ret ++;
    }
    return 9 - ret;
}

int B_ser(int k)
{
    int l = 0, r = num - 1, m;
    while(l <= r)
    {
        m = (l + r) >> 1;
        if(mp[m] == k) return m;
        else if(mp[m] > k) r = m -1;
        else l = m + 1;
    }
}

int dfs(int mk)
{
    int k = mp[mk];
    if(dp[mk] != -1) return dp[mk];
    int ret = INF, i;
    for(i = 0; i < 24; i ++)
    {
        if(((1 << i) & k) == 0)
        {
            ret = min(ret, dfs(B_ser(k | (1 << i))));
        }
    }
    if(ret == INF)
    {
        return dp[mk] = get_f(k);
    }
    return dp[mk] = get_f(k) - ret;
}

int main()
{
    //freopen("input.txt", "r", stdin);
    int a, b, n, u, v, i, j, t, cas = 1, tt, now;
    get_gogo();
    scanf("%d", &tt);
    while(tt --)
    {
        scanf("%d", &n);
        CLR(dp, -1);
        t = a = b = 0;now = 0;
        for(i = 0; i < n; i ++)
        {
            scanf("%d%d", &u, &v);
            if(u > v) swap(u, v);
            int tmd = gogo[u][v];
            t += (1 << tmd);
            int kao = 9 - get_f(t);
            if(i & 1)
            {
                b += kao - now;
                now = kao;
            }
            else
            {
                a += kao - now;
                now = kao;
            }
        }
        for(i = t, num = 0; i < (1 << 24); i ++)
        {
            if((i & t) == t)
            {
                mp[num ++] = i;
            }
        }
        if(n & 1)
        {
            b += dfs(0);
            printf("Case #%d: %s\n", cas ++, b > (9 - b) ? "Jerry404" : "Tom200");
        }
        else
        {
            a += dfs(0);
            printf("Case #%d: %s\n", cas ++, a < (9 - a) ? "Jerry404" : "Tom200");
        }
    }
}