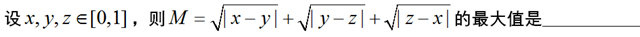
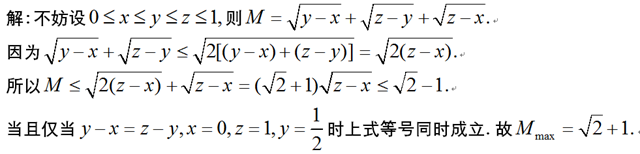
评：这是一道浙江省省赛题，这里利用对称性，设$x\le y\le z$从而解决了问题。值得注意的是此处三元轮换对称正好也是完全对称，但如果变成一般的$n\ge4$元对称问题时，就不能设大小关系。事实上有如下难题：

解答：

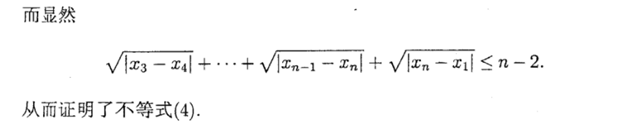
MT【98】三元对称不等式的更多相关文章

  1. 从首个IMO季军谈起 作者 : 付云皓

    刚刚过去的IMO,中国史无前例地获得了第三名,也是自1997年来近20年首次跌出前二.感谢微信等社交软件,相信现在这个新闻已经以火箭的速度传播了. 作为一个与数学竞赛及IMO打了多年交道的人,我一直有 ...

  2. MT【138】对称乎？

    已知\(a+b=1\),求\((a^3+1)(b^3+1)\)的最大值______ : 解答: \[ \begin{align*} (a^3+1)(b^3+1) &=a^3+b^3+a^3+b ...

  3. MT【25】切线不等式原理及例题

    评:切线不等式和琴生(Jesen)不等式都是有其几何意义的,在对称式中每一项单变量后利用图像的凹凸性得到一个线性的关系式.已知的条件往往就是线性条件,从而可以得到最值.

  4. MT【57】2017联赛一试解答倒数第二题:一道不等式的最值

    注:康拓诺维奇不等式的应用

  5. MT【33】证明琴生不等式

    解答:这里数学归纳法证明时指出关键的变形. 评:撇开琴生不等式自身的应用和意义外,单单就这个证明也是一道非常不错的练习数学归纳法的经典题目.

  6. MT【200】一道自招的不等式

    (2018武汉大学自招)设$x,y,z\ge0,xy+yz+zx=1$证明:$\dfrac{1}{x+y}+\dfrac{1}{y+z}+\dfrac{1}{z+x}\ge \dfrac{5}{2}$ ...

  7. MT 【331】两元非齐次不等式

    若正实数$x,y$满足$x^3+y^3=(4x-5y)y$ 则 $y$ 的最大值为____ 解答:$x^3+y^3+y^2=4(x-y)y\le x^2$,故$y^3+y^2=x^2-x^3=\dfr ...

  8. MT【327】两道不等式题

    当$x,y\ge0,x+y=2$时求下面式子的最小值:1)$x+\sqrt{x^2-2x+y^2+1}$2)$\dfrac{1}{5}x+\sqrt{x^2-2x+y^2+1}$ 解:1)$P(x,y ...

  9. MT【322】绝对值不等式

    已知 $a,b,c\in\mathbb R$,求证:$|a|+|b|+|c|+|a+b+c|\geqslant |a+b|+|b+c|+|c+a|$ 分析:不妨设$c=\max\{a,b,c\},\d ...

随机推荐

  1. Windows下配置Django环境

    辛辛苦苦,终于在Windows10上把Django环境搭建并成功建立工程 1.首先安装python,配置环境变量path:C:\Python27:C:\Python27\Scripts: 2.去dja ...

  2. Android开发——高斯模糊效果的简单实现

    0. 前言 在Android开发中,经常在音乐软件中看到高斯模糊效果. 在找遍了所有高斯模糊的算法代码后,发现stackblur的Java实现是最快的.效果如下所示. 1．  高斯模糊效果实现 Bit ...

  3. 【LG4070】[SDOI2016]生成魔咒

    [LG4070][SDOI2016]生成魔咒 题面 洛谷 题解 如果我们不用在线输的话,那么答案就是对于所有状态\(i\) \[ \sum (i.len-i.fa.len) \] 现在我们需要在线询问 ...

  4. FIFO IP核

    转载: 说白了,IP核就是别人做好了的硬件模块,提供完整的用户接口和说明文档,更复杂的还有示例工程,你只要能用好这个IP核,设计已经完成一半了.说起来容易,从冗长的英文文档和网上各个非标准教程中汲取所 ...

  5. 一步一步来熟悉Akka.Net(一）

    一步一步来熟悉Akka.Net(一) 标签(空格分隔): .netcore 分布式 一.不利flag   好久没写过文章了,翻开前几年写的博客,看到有两个目标"代码生成器"和&qu ...

  6. C语言中指针占据内存空间问题

    以前一直有个疑问,指向不同类型的指针到底占用的内存空间是多大呢? 这个问题我多次问过老师,老师的答案是"指向不同类型的指针占据的内存空间大小不同",我一直很之一这个答案,今天我就做 ...

  7. 读取配置文件的URL，使用httpClient发送Post和Get请求，实现查询快递物流和智能机器人对话

    1.主要jar包: httpclient-4.3.5.jar   httpcore-4.3.2.jar 2.目录结构如图所示: 3.url.properties文件如下: geturl=http:// ...

  8. Scrapy持久化存储

    基于终端指令的持久化存储 保证爬虫文件的parse方法中有可迭代类型对象(通常为列表or字典)的返回,该返回值可以通过终端指令的形式写入指定格式的文件中进行持久化操作; 执行输出指定格式进行存储:将爬 ...

  9. java保留两位小数4种方法（转载）

    喵喵最近经常遇到小数点保留的问题,转载一篇Java里面的几种小数点位数控制方法. 这是转载的原地址:https://www.cnblogs.com/chenrenshui/p/6128444.html ...

  10. Bloom Filter解析

    布隆过滤器简介:https://www.cnblogs.com/Jack47/p/bloom_filter_intro.html 布隆过滤器详解:原文链接:http://www.cnblogs.com ...