[转]核函数K（kernel function）

1 核函数K（kernel function）定义

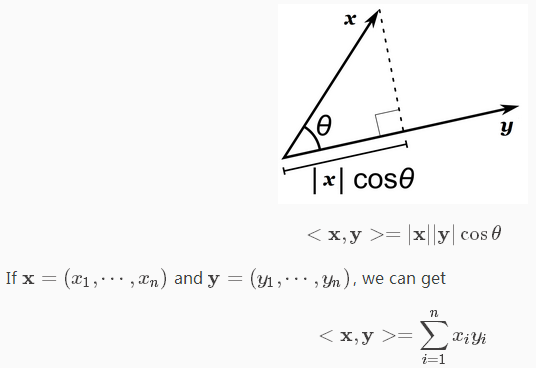
核函数K（kernel function）就是指K(x, y) = <f(x), f(y)>，其中x和y是n维的输入值，f(·) 是从n维到m维的映射（通常，m>>n）。<x, y>是x和y的内积（inner product）(也称点积（dot product）)。

举个小小栗子。
令 x = (x1, x2, x3, x4); y = (y1, y2, y3, y4);
令 f(x) = (x1x1, x1x2, x1x3, x1x4, x2x1, x2x2, x2x3, x2x4, x3x1, x3x2, x3x3, x3x4, x4x1, x4x2, x4x3, x4x4); f(y)亦然；
令核函数 K(x, y) = (<x, y>)^2.
接下来，让我们带几个简单的数字进去看看是个什么效果：x = (1, 2, 3, 4); y = (5, 6, 7, 8). 那么：
f(x) = ( 1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16) ;
f(y) = (25, 30, 35, 40, 30, 36, 42, 48, 35, 42, 49, 56, 40, 48, 56, 64) ;
<f(x), f(y)> = 25+60+105+160+60+144+252+384+105+252+441+672+160+384+672+1024
= 4900.
如果我们用核函数呢？
K(x, y) = (5+12+21+32)^2 = 70^2 = 4900.
就是这样！

所以现在你看出来了吧，kernel其实就是帮我们省去在高维空间里进行繁琐计算的“简便运算法”。甚至，它能解决无限维空间无法计算的问题！因为有时f(·)会把n维空间映射到无限维空间去。

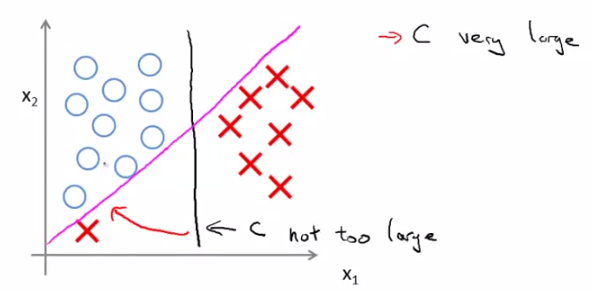
那么kernel在SVM究竟扮演着什么角色？
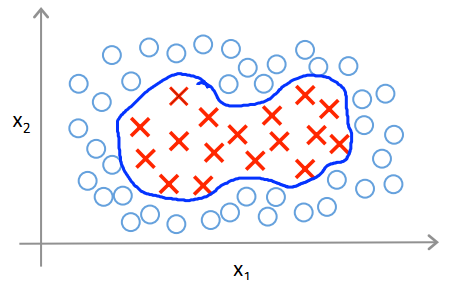
初学SVM时常常可能对kernel有一个误读，那就是误以为是kernel使得低维空间的点投射到高位空间后实现了线性可分。其实不然。这是把kernel和feature space transformation混为了一谈。（这个错误其实很蠢，只要你把SVM从头到尾认真推导一遍就不会犯我这个错。）

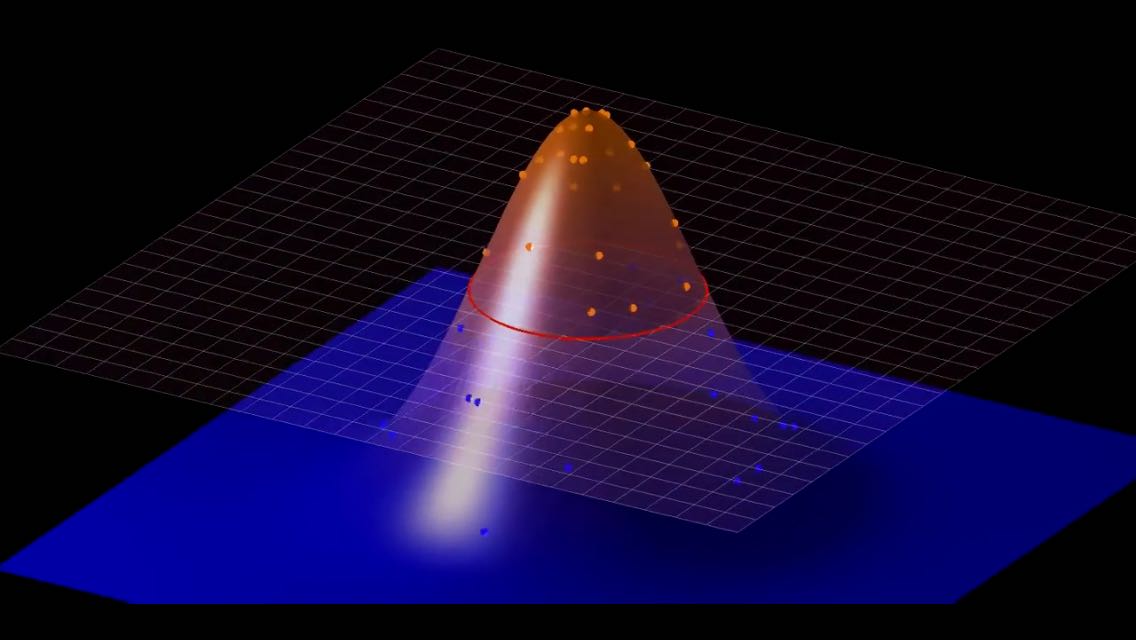
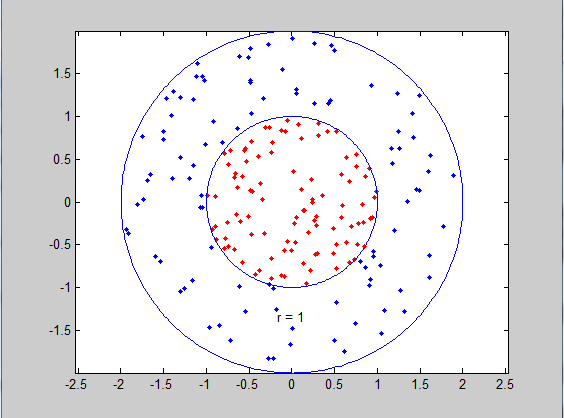
我们成功地找到了那个分界线，这就是最直观的kernel啦！
可能不太严谨，但是kernel大概就是这个意思，详细的数学定义楼上说的很好，就不赘述了。
引用一句这门课的教授的话：
“你在你的一生中可能会经历很多变故，可能会变成完全不同的另一个人，但是这个世界上只有一个你，我要怎样才能把不同的“你”分开呢？最直观的方法就是增加“时间”这个维度，虽然这个地球上只有一个你，这个你是不可分割的，但是“昨天在中国的你”和“今天在美国的你”在时间+空间这个维度却是可以被分割的。”

We know that everything in the world can be decomposed into the combination of the basic elements. For example, water is the combination of hydrogen and oxygen. Similarly, in mathematics, basis is used to represent various things in a simple and unified way.

In RnRn

space, we can use n independent vectors to represent any vector by linear combination. The n independent vectors can be viewed as a set of basis. There are infinite basis sets in RnRn

space. Among them, basis vectors that are orthogonal to each other are of special interests. For example, {ei}ni=1{ei}i=1n

is a special basis set with mutually orthogonal basis vectors in the same length, where eiei is a vector that has all zero entries except the iith entry which equals 1.
The inner product operator measures the similarity between vectors. For two vectors x and y , the inner product is the projection of one vector to the other.

3. Kernel Function

A function f(x)f(x)

can be viewed as an infinite vector, then for a function with two independent variables K(x,y)K(x,y)

, we can view it as an infinite matrix. Among them, if K(x,y)=K(y,x)K(x,y)=K(y,x)

and

∫∫f(x)K(x,y)f(y)dxdy≥0∫∫f(x)K(x,y)f(y)dxdy≥0

for any function ff

, then K(x,y)K(x,y)

is symmetric and positive definite, in which case K(x,y)K(x,y)

is a kernel function.

Here are some commonly used kernels:

Polynomial kernel K(x,y)=(γxTy+C)dK(x,y)=(γxTy+C)d
Gaussian radial basis kernel K(x,y)=exp(−γ∥x−y∥2)K(x,y)=exp⁡(−γ‖x−y‖2)
Sigmoid kernel K(x,y)=tanh(γxTy+C)K(x,y)=tanh⁡(γxTy+C)

3.1 补充知识

The hyperbolic functions are:

Hyperbolic sine:

sinhx=ex−e−x2=e2x−12ex=1−e−2x2e−x.sinh⁡x=ex−e−x2=e2x−12ex=1−e−2x2e−x.
Hyperbolic cosine:

coshx=ex+e−x2=e2x+12ex=1+e−2x2e−x.cosh⁡x=ex+e−x2=e2x+12ex=1+e−2x2e−x.
Hyperbolic tangent:

tanhx=sinhxcoshx=ex−e−xex+e−x=1−e−2x1+e−2x.tanh⁡x=sinh⁡xcosh⁡x=ex−e−xex+e−x=1−e−2x1+e−2x.

4. Reproducing Kernel Hilbert Space

Treat {λi−−√ψi}∞i=1{λiψi}i=1∞

as a set of orthogonal basis and construct a Hilbert space HH

. Any function or vector in the space can be represented as the linear combination of the basis. Suppose f=∑∞i=1fiλi−−√ψif=∑i=1∞fiλiψi

we can denote ff

as an infinite vector in HH

: f=(f1,f2,...)THf=(f1,f2,...)HT

For another function g=(g1,g2,...)THg=(g1,g2,...)HT

, we have

< f,g >H=∑∞i=1figiH=∑i=1∞figi

5. A Simple Example

6 .

线性核函数

参考文献：
[1] 机器学习里的kernel是指什么？ - 算法 - 知乎. http://www.zhihu.com/question/30371867 [2016-9-6]
[2] http://songcy.net/posts/story-of-basis-and-kernel-part-1/
[3] http://songcy.net/posts/story-of-basis-and-kernel-part-2/