hdu 2078(DFS)

Matrix

Time Limit: 2000MS		Memory Limit: 30000K
Total Submissions: 3845		Accepted: 1993

Description

Given an n*n matrix A, whose entries Ai,j are integer numbers ( 0 <= i < n, 0 <= j < n ). An operation SHIFT at row i ( 0 <= i < n ) will move the integers in the row one position right, and the rightmost integer will wrap around to the leftmost column.


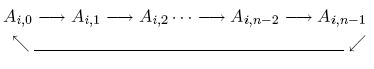
You can do the SHIFT operation at arbitrary row, and as many times as you like. Your task is to minimize

max_{0<=j< n}{Cj|Cj=Σ_{0<=i< n}A_i,j}

Input

The
input consists of several test cases. The first line of each test case
contains an integer n. Each of the following n lines contains n
integers, indicating the matrix A. The input is terminated by a single
line with an integer −1. You may assume that 1 <= n <= 7 and |A_i,j| < 10⁴.

Output

For each test case, print a line containing the minimum value of the maximum of column sums.

Sample Input

2
4 6
3 7
3
1 2 3
4 5 6
7 8 9
-1

Sample Output

11
15

题意:一个矩阵经过变换之后（变换规则如上图）,每次都有一个每一列的最大值，现在求解所有的这些变换中最大值的最小值。
题解:最多7^7。。所以深搜。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<math.h>
#include<queue>
#include<iostream>
using namespace std;
const int INF = ;
int M[][];
int n,res;

int now(){
    int MAX = -INF;
    for(int i=;i<=n;i++){
        int sum = ;
        for(int j=;j<=n;j++){
            sum=sum+M[j][i];
        }
        if(sum>MAX) MAX = sum;
    }
    return MAX;
}
void _move(int k){ ///移动第k行
    int temp = M[k][n];
    for(int i=n;i>;i--){
        M[k][i] = M[k][i-];
    }
    M[k][] = temp;
}
void dfs(int step){ ///当前移动第step行
    if(step==n+) {
        return;
    }
    int MAX = now();
    if(MAX<res) res = MAX;
    for(int i=;i<=n;i++){ #移动 n 次枚举该行移动的所有状态
        _move(step);
        dfs(step+);
    }
}

int main()
{
    while(scanf("%d",&n)!=EOF,n!=-){
        res = INF;
        for(int i=;i<=n;i++){
            for(int j=;j<=n;j++){
                scanf("%d",&M[i][j]);
            }
        }
        dfs();
        printf("%d\n",res);
    }
    return ;
}