[leetcode]426. Convert Binary Search Tree to Sorted Doubly Linked List二叉搜索树转有序双向链表
Convert a BST to a sorted circular doubly-linked list in-place. Think of the left and right pointers as synonymous to the previous and next pointers in a doubly-linked list.
Let's take the following BST as an example, it may help you understand the problem better:

We want to transform this BST into a circular doubly linked list. Each node in a doubly linked list has a predecessor and successor. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.
The figure below shows the circular doubly linked list for the BST above. The "head" symbol means the node it points to is the smallest element of the linked list.
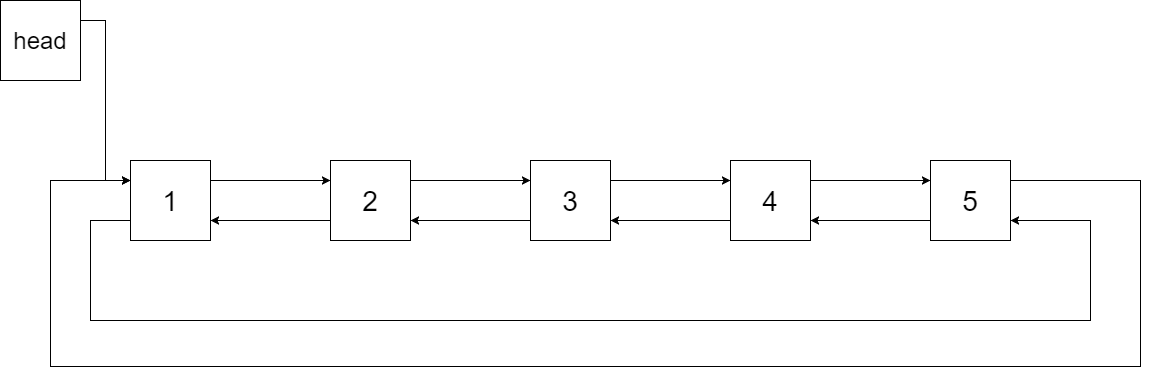
Specifically, we want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. We should return the pointer to the first element of the linked list.
The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship.
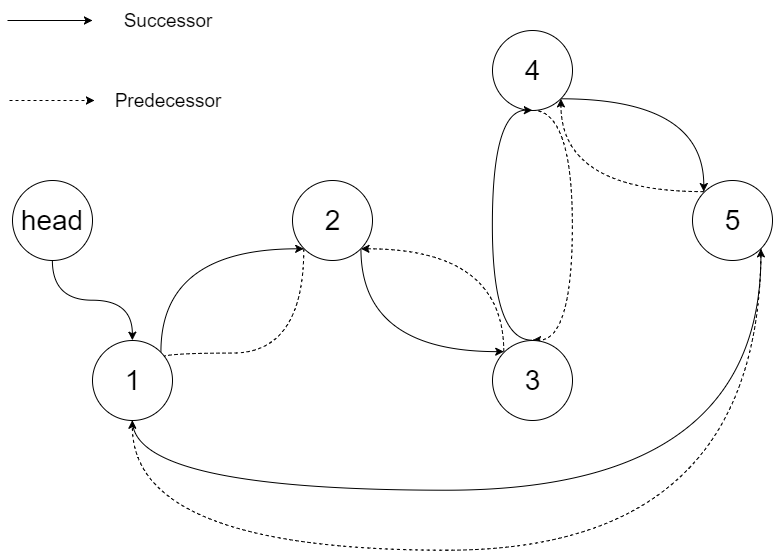
[leetcode]426. Convert Binary Search Tree to Sorted Doubly Linked List二叉搜索树转有序双向链表的更多相关文章
- LeetCode 426. Convert Binary Search Tree to Sorted Doubly Linked List
原题链接在这里:https://leetcode.com/problems/convert-binary-search-tree-to-sorted-doubly-linked-list/ 题目: C ...
- 【LeetCode】426. Convert Binary Search Tree to Sorted Doubly Linked List 解题报告 (C++)
作者: 负雪明烛 id: fuxuemingzhu 个人博客:http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题方法 递归 迭代 日期 题目地址:https://leetc ...
- 426. Convert Binary Search Tree to Sorted Doubly Linked List把bst变成双向链表
[抄题]: Convert a BST to a sorted circular doubly-linked list in-place. Think of the left and right po ...
- [LC] 426. Convert Binary Search Tree to Sorted Doubly Linked List
Convert a BST to a sorted circular doubly-linked list in-place. Think of the left and right pointers ...
- [LeetCode] Convert Binary Search Tree to Sorted Doubly Linked List 将二叉搜索树转为有序双向链表
Convert a BST to a sorted circular doubly-linked list in-place. Think of the left and right pointers ...
- LeetCode426.Convert Binary Search Tree to Sorted Doubly Linked List
题目 Convert a BST to a sorted circular doubly-linked list in-place. Think of the left and right point ...
- [LeetCode] 272. Closest Binary Search Tree Value II 最近的二叉搜索树的值 II
Given a non-empty binary search tree and a target value, find k values in the BST that are closest t ...
- [LeetCode#272] Closest Binary Search Tree Value II
Problem: Given a non-empty binary search tree and a target value, find k values in the BST that are ...
- [LeetCode] Trim a Binary Search Tree 修剪一棵二叉搜索树
Given a binary search tree and the lowest and highest boundaries as L and R, trim the tree so that a ...
随机推荐
- [UE4]Acotr
任何能被放在关卡中的对象都是Actor Tick是每帧都会调用的事件
- Mybatis -代码自动生成(generatorConfig.xml)
参考:http://blog.csdn.net/jinshiyill/article/details/51546676 官方网址: http://www.mybatis.org/generator/c ...
- java 泛型中 T 和 问号(通配符)的区别
类型本来有:简单类型和复杂类型,引入泛型后把复杂类型分的更细了: 现在List<Object>, List<String>是两种不同的类型;且无继承关系: 泛型的好处如: 开始 ...
- Hadoop 2.7.3 分布式集群安装
1. 集群规划: 192.168.1.252 palo252 Namenode+Datanode 192.168.1.253 palo253 YarnManager+Datanode+Secondar ...
- OpenGL chapter3 基础渲染
3.1 基础图形管线 三种向OpenGl着色器传递渲染数据的方法:属性,Uniform和纹理.3.2 创建坐标系 3.2.1 正投影 GLFrustum::SetOrthographic(⋯⋯): 3 ...
- Spark数据本地性
1.文件系统本地性 第一次运行时数据不在内存中,需要从HDFS上取,任务最好运行在数据所在的节点上: 2.内存本地性 第二次运行,数据已经在内存中,所有任务最好运行在该数据所在内存的节点上: 3.LR ...
- 洛谷 P2054 [AHOI2005]洗牌
题目描述 为了表彰小联为Samuel星球的探险所做出的贡献,小联被邀请参加Samuel星球近距离载人探险活动. 由于Samuel星球相当遥远,科学家们要在飞船中度过相当长的一段时间,小联提议用扑克牌打 ...
- 为github帐号添加SSH keys(Linux和Windows)
文章转自:https://blog.cofface.com/archives/406.html/2 一.Linux增加ssh keys方法: 使用git clone命令从github上同步github ...
- 开启saltstack的web界面
saltstack官方有提供一个web界面叫halite,halite是用cherrypy web框架开发的,连接后端的saltstack api,web界面虽然简单点,但功能还算齐全,今天就来开启s ...
- leetcode941
public class Solution { public bool ValidMountainArray(int[] A) { bool findTop = false; ) { return f ...
